题目内容
宁波滨海水产城一养殖专业户陈某承包了30亩水塘,分别养殖甲鱼和桂鱼.有关成本、销售额见下表:

(1)2011年,陈某养殖甲鱼20亩,桂鱼10亩.求陈某这一年共收益多少万元?(收益=销售额-成本)
(2)2012年,陈某继续用这30亩水塘全部养殖甲鱼和桂鱼,计划投入成本不超过70万元.若每亩养殖的成本、销售额与2011年相同,要获得最大收益,他应养殖甲鱼和桂鱼各多少亩?
(3)已知甲鱼每亩需要饲料500kg,桂鱼每亩需要饲料700kg.根据(2)中的养殖亩数,为了节约运输成本,实际使用的运输车辆每次装载饲料的总量是原计划每次装载总量的2倍,结果运输养殖所需全部饲料比原计划减少了2次.求陈某原定的运输车辆每次可装载饲料多少kg?

(1)2011年,陈某养殖甲鱼20亩,桂鱼10亩.求陈某这一年共收益多少万元?(收益=销售额-成本)
(2)2012年,陈某继续用这30亩水塘全部养殖甲鱼和桂鱼,计划投入成本不超过70万元.若每亩养殖的成本、销售额与2011年相同,要获得最大收益,他应养殖甲鱼和桂鱼各多少亩?
(3)已知甲鱼每亩需要饲料500kg,桂鱼每亩需要饲料700kg.根据(2)中的养殖亩数,为了节约运输成本,实际使用的运输车辆每次装载饲料的总量是原计划每次装载总量的2倍,结果运输养殖所需全部饲料比原计划减少了2次.求陈某原定的运输车辆每次可装载饲料多少kg?
(1)17万元;(2)甲鱼25亩,桂鱼5亩;(3)4000kg
试题分析:(1)仔细分析题意及表中数据即可列算式求解;
(2)先设养殖甲鱼x亩,则养殖桂鱼(30-x)亩列不等式,求出x的取值,再表示出陈某可获得收益为y万元函数关系式求最大值;
(3)设陈某原定的运输车辆每次可装载饲料a㎏,结合(2)列分式方程求解.
(1)
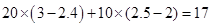 (万元)
(万元)答:陈某这一年共收益17万元;
(2)设甲鱼养殖
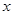 亩,则养殖桂鱼
亩,则养殖桂鱼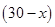 亩,
亩,由题意知
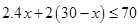
解得
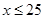
设收益为
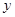 万元,则
万元,则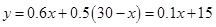
∵函数值y随x的增大而增大,
∴当
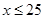 时,
时,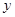 最大值17.5万元
最大值17.5万元答:要获得最大收益,应养殖甲鱼25亩,桂鱼5亩;
(3)设陈某原定的运输车辆每次可装载饲料a㎏,
由(2)得,共需要饲料为500×25+700×5=16000(㎏),
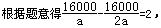
解得a=4000,
把a=4000代入原方程公分母得,2a=2×4000=8000≠0,
故a=4000是原方程的解.
答:陈某原定的运输车辆每次可装载饲料4000㎏.
点评:解题的关键是列不等式求x的取值范围,再表示出函数关系求最大值,再列分式方程求解.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目


 的图象如图所示.
的图象如图所示.
 ,求二次函数的解析式;
,求二次函数的解析式; ,点
,点 是x轴上的一个动点.若在(1)的条件下,过点P垂直于x轴的直线交这个一次函数的图象于点M,交二次函数
是x轴上的一个动点.若在(1)的条件下,过点P垂直于x轴的直线交这个一次函数的图象于点M,交二次函数 时,点M位于点N的上方,求这个一次函数的解析式;
时,点M位于点N的上方,求这个一次函数的解析式; 有实数根,请你构造恰当的函数,根据图象直接写出
有实数根,请你构造恰当的函数,根据图象直接写出 的最大值.
的最大值. 的图象,如图所示,当
的图象,如图所示,当 时,
时, 的取值范围是( )
的取值范围是( )




 分别交
分别交 轴、
轴、 轴于
轴于 两点.点
两点.点 、
、 ,以
,以 为一边在
为一边在 ,且
,且 .设矩形
.设矩形 重叠部分的面积为
重叠部分的面积为 .
.
 、
、 的坐标;
的坐标; 值由小到大变化时,求
值由小到大变化时,求 ,使
,使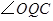 等于
等于 ,请直接写出
,请直接写出

