题目内容
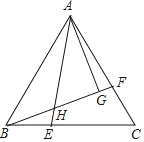
【题目】在等边三角形ABC中,点F是线段AC上一点,点E是线段BC上一点,BF与AE交于点H,∠BAE=∠FBC,AG⊥BF,∠GAF:∠BEA=1:10,则∠BAE=_____°.
【答案】20
【解析】
由△ABE≌△BCF(ASA),推出∠AEB=∠BFC,由题意可以假设∠GAF=x,则∠AEB=∠BFC=10x,由∠AGF=90°,可得∠GAF+∠AFG=90°,由此构建方程求出x即可解决问题.
∵△ABC是等边三角形,
∴AB=BC,∠ABE=∠C=60°,
∵∠BAE=∠FBC,
∴△ABE≌△BCF(ASA),
∴∠AEB=∠BFC,
∵∠GAF:∠BEA=1:10,
∴可以假设:∠GAF=x,则∠AEB=∠BFC=10x,
∵AG⊥BF,
∴∠AGF=90°,
∴∠GAF+∠AFG=90°,
∴x+(180°-10x)=90°,
∴x=10°,
∴∠AEB=100°,
∴∠BAE=180°-60°-100°=20°,
故答案为20.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目