题目内容
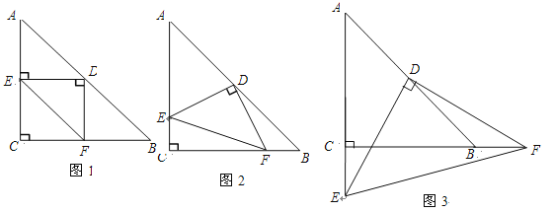
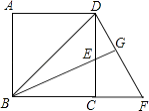
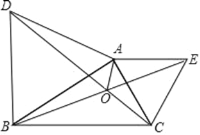
【题目】如图,分别以△ABC 的边 AB,AC 向外作等边三角形 ABD 和等边三角形 ACE,线段 BE 与 CD 相交于点 O,连接 OA.
(1)求证:BE=DC;
(2)求∠BOD 的度数;
(3)求证:OA 平分∠DOE.
(4)猜想线段 OA、OB、OD 的数量关系,并证明.
【答案】(1)见解析;(2) 60°;(3)见解析;(4)见解析.
【解析】
(1)根据等边三角形性质得出AB=AD,AE=AC,∠BAD=∠BDA=∠DBA=∠CAE=60°,求出∠BAE=∠DAC.根据SAS证△ABE≌△ADC即可;(2)根据全等求出∠ADC=∠ABE,在△DOB中根据三角形的内角和定理和∠ADB=∠DBA=60°即可求出答案;
(3)过点A分别作AM⊥BE,AN⊥DC,垂足为点M,N.根据三角形的面积公式求出AN=AM,根据角平分线性质求出即可;(4)在 OD 上截取一点 G,使得 OG=OA.由(2)(3)知∠AOD=∠BOD=∠AOE=60°,故可证△AOG 是等边三角形,根据等边三角形性质得到AG=AO,∠GAO=60°,进而得到∠DAG=∠BAO,根据SAS证△DAG≌△BAO,进而可得OD=OG+DG=OA+OB.
(1)证明:∵△ABD 和△ACE 都是等边三角形,
∴ AB=AD,AE=AC,∠BAD=∠BDA=∠DBA=∠CAE=60°,
∴∠BAC+∠CAE=∠BAC+∠BAD, 即∠BAE=∠DAC.
在△ABE 和△ADC 中
∵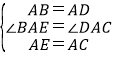 ,
,
∴△ABE≌△ADC(SAS),
∴BE=DC.
(2)解:由(1)知:△ABE≌△ADC,
∴∠ADC=∠ABE
∴∠ADC+∠BDO=∠ABE+∠BDO=∠BDA=60°
∴在△BOD 中,∠BOD=180°﹣∠BDO﹣∠DBA﹣∠ABE
=180°﹣∠DBA﹣(∠ADC+∠BDO)
=180°﹣60°﹣60°
=60°.
(3)证明:过点 A 分别作 AM⊥BE,AN⊥DC,垂足为点 M,N.
∵由(1)知:△ABE≌△ADC,
∴S△ABE=S△ADC
∴![]() BEAM=
BEAM=![]() DCAN
DCAN
∴AM=AN
∴点 A 在∠DOE 的平分线上, 即 OA 平分∠DOE.
(4)解:结论:OD=OA+OB.
理由:在 OD 上截取一点 G,使得 OG=OA.
由(2)(3)可知:∠AOD=∠BOD=∠AOE=60°,
∵OG=OA,
∴△AOG 是等边三角形,
∴AG=AO,∠GAO=60°,
∵∠DAB=∠GAO=60°,
∴∠DAG=∠BAO,
∵AD=AB,AG=AO,
∴△DAG≌△BAO(SAS),
∴DG=BO,
∴OD=OG+DG=OA+OB.