Question

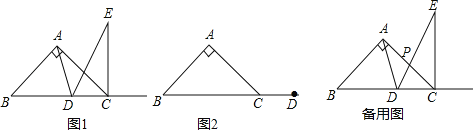
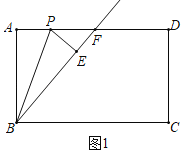
【题目】如图，矩形ABCD中，点P为AD上一个动点，以PB 为对称轴将△APB折叠得到△EPB，点A的对称点为点E，射线BE交矩形ABCD的边于点 F，若AB＝4，AD＝6，当点F为矩形ABCD边的中点时，AP的长为_____．

Answer 1

【答案】或．

【解析】

分两种情形：如图1中，当点F是AD的中点时．如图2中，当点F是CD的中点时，延长AD交BF的延长线于H．分别求解即可．

解：如图1中，当点F是AD的中点时，

∵四边形ABCD是矩形，

∴∠A＝90°，AB＝6，AF＝3，

∴BF＝＝＝5，

由翻折可知：AB＝BE＝4，设PA＝PE＝x，则PF＝3﹣x，EF＝5﹣4＝1，

在Rt△PEF中，∵PE2+EF2＝PF2，

∴x2+12＝（3﹣x）2，

∴x＝，

∴PA＝

如图2中，当点F是CD的中点时，延长AD交BF的延长线于H．

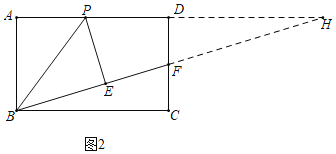
∵∠C＝90°，BC＝6，CF＝DF＝2，

∴BF＝＝2，

∵DH∥BC，

∴∠H＝∠FBC，

∵∠DFH＝∠BFC，DF＝FC，

∴△DHF≌△CBF（AAS），

∴DH＝BC＝6，FH＝BF＝2，

∵AB＝BE＝4，

∴EF＝2﹣4，EH＝2﹣4+2＝4﹣4，

设PA＝PE＝y，则PD＝6﹣y，PH＝6﹣y+6＝12﹣y，

在Rt△PEH中，∵PE2+EH2＝PH2，

∴y2+（4﹣4）2＝（12﹣y）2，

∴y＝，

∴PA＝，

综上所述，PA的长为或．

故答案为：或．