题目内容
若二次函数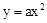 的图象经过点P(2,8),则该图象必经过点
的图象经过点P(2,8),则该图象必经过点
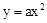 的图象经过点P(2,8),则该图象必经过点
的图象经过点P(2,8),则该图象必经过点| A.(2,-8) | B.(-2,8) | C.(8,-2) | D.(-8,2) |
B.
试题分析:∵二次函数
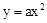 的图象经过点P(2,8),∴
的图象经过点P(2,8),∴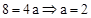 .
.∴二次函数解析式为
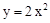 .∴该图象必经过点(-2,8).
.∴该图象必经过点(-2,8).故选B.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
题目内容
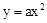 的图象经过点P(2,8),则该图象必经过点
的图象经过点P(2,8),则该图象必经过点| A.(2,-8) | B.(-2,8) | C.(8,-2) | D.(-8,2) |
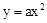 的图象经过点P(2,8),∴
的图象经过点P(2,8),∴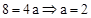 .
.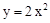 .∴该图象必经过点(-2,8).
.∴该图象必经过点(-2,8).
 学业测评一课一测系列答案
学业测评一课一测系列答案