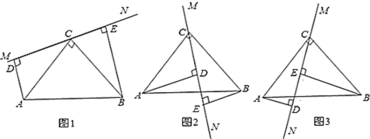
��Ŀ����
����Ŀ�����ɶ������ض��������֤�����������еġ������������������У�����ϲ�ط��֣�������ȫ�ȵ�ֱ����������ͼ��1���ڷ�ʱ�����������������֤�����ɶ�������������
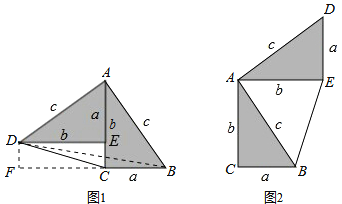
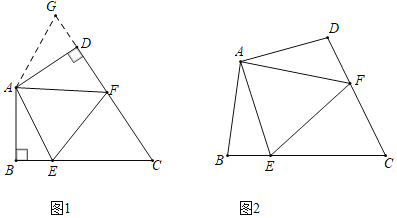
��ͼ��1����DAB=90�㣬��֤��a2+b2=c2
֤��������DB������D��DF��BC��BC���ӳ����ڵ�F����DF=b-a
S�ı���ADCB=![]()
S�ı���ADCB=![]()
��![]() ����ã�a2+b2=c2
����ã�a2+b2=c2
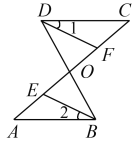
���������֤�������á�������������ͼ��2���Ĺ��ɶ�����֤������ͼ��2���С�DAB=90�㣬��֤��a2+b2=c2
���𰸡�������.
��������
��������BD������B��DE���ϵĸ�BF����BF=b-a����ʾ��S�����ACBED��������ȣ��������ɵ�֤��
֤��������BD������B��DE���ϵĸ�BF����BF=b-a��
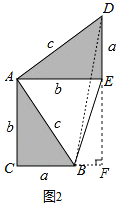
��S�����ACBED=S��ACB+S��ABE+S��ADE=![]() ab+
ab+![]() b2+
b2+![]() ab��
ab��
�֡�S�����ACBED=S��ACB+S��ABD+S��BDE=![]() ab+
ab+![]() c2+
c2+![]() a��b-a����
a��b-a����
��![]() ab+
ab+![]() b2+
b2+![]() ab=
ab=![]() ab+
ab+![]() c2+
c2+![]() a��b-a����
a��b-a����
��a2+b2=c2��

��ϰ��ϵ�д�
�����Ŀ