��Ŀ����
����Ŀ���Ķ����в��ϣ�������⣺
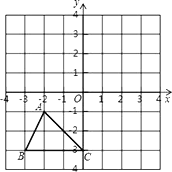
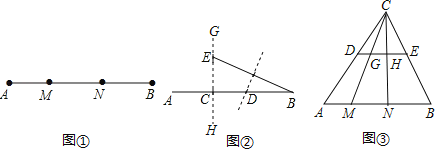
ѧϰ�˹��ɶ���������֪����ֱ������������ֱ�DZߵ�ƽ���͵���б�ߵ�ƽ�������ݹ��ɶ������Ƕ��壺��ͼ�٣���M��N���߶�AB�����㣬����߶�AM��MN��NB�ܹ���ֱ�������Σ���Ƶ�M��N���߶�AB�Ĺ��ɵ�
�������
��1����ͼ���У����AM��2��MN��3����NB���� ����
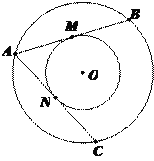
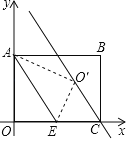
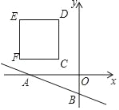
��2����ͼ�ڣ���֪��C���߶�AB��һ���㣨AC��BC�������߶�AB������һ��D��ʹ��C��D���߶�AB�Ĺ��ɵ㣮����ͬѧ���������ģ�����C��ֱ��GH��AB����GH�Ͻ�ȡCE��AC������BE����BE�Ĵ�ֱƽ���߽�AB�ڵ�D����C��D���߶�AB�Ĺ��ɵ�����Ϊ����ͬѧ������������˵������
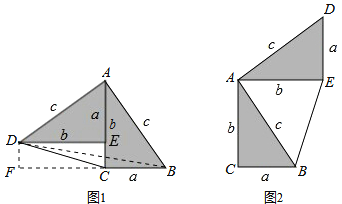
��3����ͼ�ۣ�DE�ǡ�ABC����λ�ߣ�M��N��AB�ߵĹ��ɵ㣨AM��MN��NB��������CM��CN�ֱ�DE�ڵ�G��H��֤��G��H���߶�DE�Ĺ��ɵ㣮
���𰸡���1��![]() ��
��![]() ����2���ԣ����ɼ���������3��������
����2���ԣ����ɼ���������3��������
��������
��1�����������ηֱ���⼴�ɽ�����⣮
��2����취֤��DB2��AC2+CD2���ɣ�
��3�����������ε���λ�߶����Լ����ɶ���֤��EH2��GH2+DG2���ɣ�
�⣺��1����BN��б��ʱ��BN��![]() ��
��![]() ��
��
��MN��б��ʱ��BN��![]() ��
��![]() ��
��
�ʴ�Ϊ![]() ��
��![]() ��
��
��2����ͼ���У�����DE��

�ߵ�D���߶�BE�Ĵ�ֱƽ�����ϣ�
��DE��DB��
��GH��BC��
���ECD��90�㣬
��DE2��EC2+CD2��
��AC��CE��DE��DB��
��DB2��AC2+CD2��
��C��D���߶�AB�Ĺ��ɵ㣮
��3����ͼ3�У�
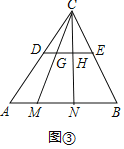
��CD��DA��CE��EB��
��DE��AB��
��CG��GM��CH��HN��
��DG��![]() AM��GH��
AM��GH��![]() MN��EH��
MN��EH��![]() BN��
BN��
��BN2��MN2+AM2��
��![]() BN2��
BN2��![]() MN2+
MN2+![]() AM2��
AM2��
�ࣨ![]() BN��2����
BN��2����![]() MN��2+��
MN��2+��![]() AM��2��
AM��2��
��EH2��GH2+DG2��
��G��H���߶�DE�Ĺ��ɵ㣮