题目内容
【题目】填写下列证明过程中的推理根据：
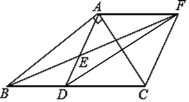
已知：如图所示，AC，BD相交于O，DF平分∠CDO与AC相交于F，BE平分于∠ABO与AC相交于E，∠A＝∠C.求证：∠1＝∠2.
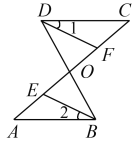
证明：∵∠A＝∠C(________)，
∴AB∥CD (__________________________________)，
∴∠ABO＝∠CDO (__________________________________)，
又∵∠1＝
CDO，∠2＝∠ABO (__________________________________)，
∴∠1＝∠2(____________________)．
【答案】已知 ；内错角相等，两直线平行；两直线平行，内错角相等；角平分线定义；等量代换
【解析】
由∠A＝∠C判定AB∥CD，再由平行线的性质推出∠ABO＝∠CDO，然后由角平分线的性质证得∠1＝∠2。
证明：∵∠A＝∠C(已知)，
∴AB∥CD (内错角相等，两直线平行)，
∴∠ABO＝∠CDO (两直线平行，内错角相等)，
又∵∠1＝
CDO，∠2＝∠ABO (角平分线定义)，
∴∠1＝∠2(等量代换)．
故答案为：已知 ；内错角相等，两直线平行；两直线平行，内错角相等；角平分线定义；等量代换
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
