题目内容
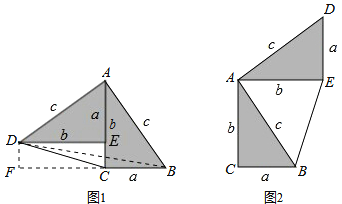
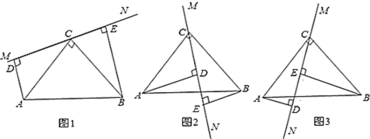
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,且
,且![]() 于点
于点![]() ,
,![]() 于点
于点![]() .易得
.易得![]() (不需要证明).
(不需要证明).
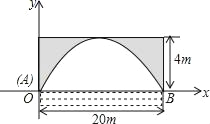
(1)当直线![]() 绕点
绕点![]() 旋转到图2的位置时,其余条件不变,你认为上述结论是否成立?若成立,写出证明过程;若不成立,请写出此时
旋转到图2的位置时,其余条件不变,你认为上述结论是否成立?若成立,写出证明过程;若不成立,请写出此时![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(2)当直线![]() 绕点
绕点![]() 旋转到图3的位置时,其余条件不变,请直接写出此时
旋转到图3的位置时,其余条件不变,请直接写出此时![]() 之间的数量关系(不需要证明).
之间的数量关系(不需要证明).
【答案】(1) 不成立,DE=AD-BE,理由见解析;(2) DE=BE-AD
【解析】
(1)DE、AD、BE之间的数量关系是DE=AD-BE.由垂直的性质可得到∠CAD=∠BCE,证得△ACD≌△CBE,得到AD=CE,CD=BE,即有DE=AD-BE;
(2)DE、AD、BE之间的关系是DE=BE-AD.证明的方法与(1)一样.
(1)不成立.
DE、AD、BE之间的数量关系是DE=AD-BE,
理由如下:如图,
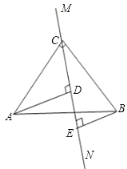
∵∠ACB=90°,BE⊥CE,AD⊥CE,![]() ,
,
∴∠ACD+∠CAD=90°,
又∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
在△ACD和△CBE中,
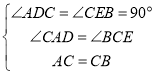 ,
,
∴△ACD≌△CBE(AAS),
∴AD=CE,CD=BE,
∴DE=CE-CD=AD-BE;
(2)结论:DE=BE-AD.
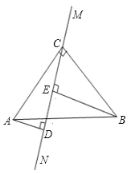
∵∠ACB=90°,BE⊥CE,AD⊥CE,![]() ,
,
∴∠ACD+∠CAD=90°,
又∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
在△ACD和△CBE中,
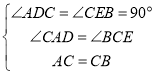 ,
,
∴△ADC≌△CEB(AAS),
∴AD=CE,DC=BE,
∴DE=CD-CE=BE-AD.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目