题目内容
【题目】已知:关于x的方程:mx2﹣(3m﹣1)x+2m﹣2=0.
(1)求证:无论m取何值时,方程恒有实数根;
(2)若关于x的二次函数y=mx2﹣(3m﹣1)x+2m﹣2的图象与x轴两交点间的距离为2时,求抛物线的解析式.
【答案】(1)分![]() 与
与![]() 两种情况讨论,再结合一元二次方程的根的判别式即可判断;
两种情况讨论,再结合一元二次方程的根的判别式即可判断;
(2)![]()
【解析】
试题(1)、分两种情况讨论:①当m=0时,方程为一元一次方程,若能求出解,则方程有实数根;
②当m≠0时,方程为一元二次方程,计算出△的值为非负数,可知方程有实数根.(2)、根据二次函数与x轴的交点间的距离公式,求出m的值,从而得到抛物线的解析式.
试题解析:(1)、①当m=0时,原方程可化为x﹣2=0,解得x=2;②当m≠0时,方程为一元二次方程,
△=[﹣(3m﹣1)]2﹣4m(2m﹣2) =m2+2m+1 =(m+1)2≥0,故方程有两个实数根;
故无论m为何值,方程恒有实数根.
(2)、∵二次函数y=mx2﹣(3m﹣1)x+2m﹣2的图象与x轴两交点间的距离为2,
∴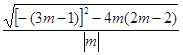 =2, 整理得,3m2﹣2m﹣1=0, 解得m1=1,m2=﹣
=2, 整理得,3m2﹣2m﹣1=0, 解得m1=1,m2=﹣![]() .
.
则函数解析式为y=x2﹣2x或y=﹣![]() x2+2x﹣
x2+2x﹣![]() .
.

练习册系列答案
相关题目