题目内容
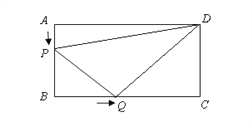
【题目】如图所示,在长方形ABCD中,AB=6厘米,BC=12厘米,点P沿AB边从点A开始向点B以1厘米/秒的速度移动,点Q沿BC从点B开始向点C以2厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).
(1)当PB=2厘米时,求点P移动多少秒?
(2)t为何值时,△PBQ为等腰直角三角形?
(3)求四边形PBQD的面积,并探究一个与计算结果有关的结论.
【答案】(1)4;(2)2;(3)36,不论P、Q怎样运动总有四边形PBQD的面积等于长方形ABCD面积的一半
【解析】试题分析:(1)由AB、PB的长可求得AP的长,则可求得t的值;
(2)根据等腰直角三角形的性质可求得PB=BQ,则可得到关于t的方程,可求得t的值;
(3)可用t分别表示出S△APD、S△QCD,再利用面积的和差可求得四边形PBQD的面积,则可求得结论.
试题解析:
(1)∵PB=2cm,AB=6cm,
∴AP=AB-PB=6-2=4(秒),
即点P移动4秒;
(2)∵△PBQ为等腰直角三角形,
∴PB=BQ,即6-t=2t,解得t=2,
∴当t的值为2秒时,△PBQ为等腰直角三角形;
(3)由题意可知AP=t,AB=6,BQ=2t,BC=12,
∴PB=6-t,QC=12-2t,CD=6,AD=12,
∴S△APD=![]() APAD=
APAD=![]() t×12=6t,
t×12=6t,
S△QCD=![]() QCCD=
QCCD=![]() (12-2t)6=36-6t,
(12-2t)6=36-6t,
∴S四边形PBQD=S矩形ABCD-S△APD-S△QCD=72-6t-(36-6t)=36,
结论:不论P、Q怎样运动总有四边形PBQD的面积等于长方形ABCD面积的一半.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目