题目内容
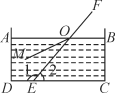
【题目】如图，在边长为4的正方形ABCD中，E为AD的中点，F为BC边上一动点，设BF=t（0≤t≤2），线段EF的垂直平分线GH分别交边CD，AB于点G，H，过E做EM⊥BC于点M，过G作GN⊥AB于点N．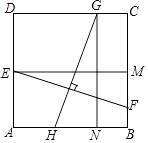 
（1）当t≠2时，求证：△EMF≌△GNH；
（2）顺次连接E、H、F、G，设四边形EHFG的面积为S，求出S与自变量t之间的函数关系式，并求S的最小值．
【答案】
（1）解：
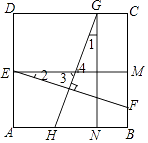
证明：∵四边形ABCD是正方形，EM⊥BC，GN⊥AB，
∴EM=GN=AB=AD，
∵∠1+∠4=90°，∠2+∠3=90°，∠3=∠4，
∴∠1=∠2，
在△EMF和△GNH中，
，
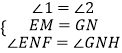∴△EMF≌△GNH．
（2）解：∵△EMF≌△GNH，
∴EF=GH，
∵BF=t，BM=2，
∴FM=2﹣t，
∴EF2=42+（2﹣t）2，
∵S= 
EFGH= （x﹣2）2+8，
∵0≤t≤2，
∴t=2时，S有最小值，最小值为8．
【解析】（1）只要证明EM=GN，∠1=∠2，即可利用ASA证明．（2）根据S= EFGH计算，利用二次函数的性质即可解决问题．
练习册系列答案
相关题目
