题目内容
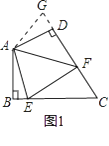
【题目】如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD= ![]() ,CD=
,CD= ![]() ,点P在四边形ABCD上,若P到BD的距离为
,点P在四边形ABCD上,若P到BD的距离为 ![]() ,则点P的个数为( )
,则点P的个数为( ) 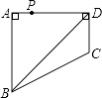
A.1
B.2
C.3
D.4
【答案】B
【解析】解:过点A作AE⊥BD于E,过点C作CF⊥BD于F, 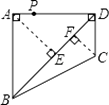
∵∠BAD=∠ADC=90°,AB=AD= ![]() ,CD=
,CD= ![]() ,
,
∴∠ABD=∠ADB=45°,
∴∠CDF=90°﹣∠ADB=45°,
∵sin∠ABD= ![]() ,
,
∴AE=ABsin∠ABD=2 ![]() sin45°
sin45°
=2 ![]()
![]() =2>
=2> ![]() ,
,
所以在AB和AD边上有符合P到BD的距离为 ![]() 的点2个,
的点2个,
∵sin∠CDF= ![]() ,
,
∴CF=CDsin∠CDF= ![]()
![]() =1<
=1< ![]() ,
,
所以在边BC和CD上没有到BD的距离为 ![]() 的点,
的点,
总之,P到BD的距离为 ![]() 的点有2个.
的点有2个.
故选:B.
【考点精析】解答此题的关键在于理解点到直线的距离的相关知识,掌握从直线外一点到这条直线的垂线段的长度叫做点到直线的距离,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
相关题目