Question

【题目】如图，在△ABC 中，AB＝AC，∠BAC＝120°，D 为 BC 的中点，DE⊥AC 于点 E，AE＝8，求 CE 的长．

Answer 1

【答案】CE＝24．

【解析】

连接 AD，利用等边对等角得∠B＝∠C＝30°, 在 Rt△ADE 中，得AD＝16，在 Rt△ADC 中，得AC＝32，即可求出CE的长.

连接 AD，

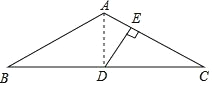
∵AB＝AC，∠BAC＝120°，D 为 BC 的中点，

∴AD⊥BC，AD 平分∠BAC，∠B＝∠C＝30°

∴∠DAC＝ ∠BAC＝60°，

∵DE⊥AC 于 E，

∴∠AED＝90°，

∴∠ADE＝30°，

在 Rt△ADE 中，AE＝2，∠ADE＝30°，

∴AD＝2AE＝16，

在 Rt△ADC 中，AD＝4，∠C＝30°，

∴AC＝2AD＝32，

则 CE＝AC﹣AE＝32﹣8＝24．