题目内容
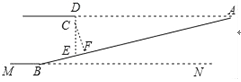
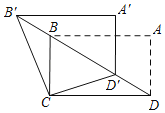
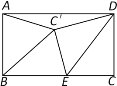
【题目】如图,在矩形ABCD中,AB=2,AD=4,点E在边BC上,把△DEC沿DE翻折后,点C落在C′处.若△ABC′恰为等腰三角形,则CE的长为__________.
【答案】2或![]()
【解析】
根据△ABC′恰为等腰三角形分两种情况进行分类讨论,①当C′A=C′B时,根据翻折的性质和勾股定理可求出DH,再根据“K”型相似,易得△DHC′∽△C′FE即可求出,②当AB=AC′时,此时四边形CEC′D是正方形易得出答案.
如图1中,当C′A=C′B时,作C′H⊥AD于H交BC于F,
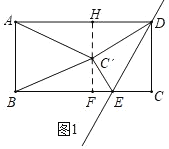
易知HC′=FC′=1,在Rt△DHC′中,![]() ,
,
由△DHC′∽△C′FE,可得:![]() ,
,
∴![]() ,
,
∴EF=![]() ,
,
∵四边形DHFC是矩形,
∴CF=DH=![]() ,
,
∴![]() ,
,
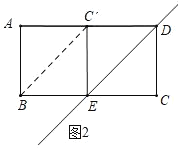
如图2中,当AB=AC′时,点C′在AD上,此时四边形CEC′D是正方形,CE=2,
故答案为:2或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
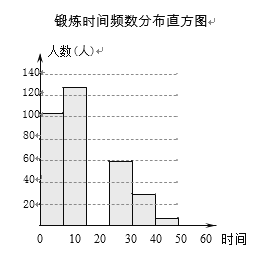
【题目】某数学活动小组为了解全县九年级学生在抗新冠病毒疫情期间平均每天居家锻炼时间,向全县部分学生进行了抽样调查,并将收集到的数据整理成如图的统计图(部分数据未标出).
(1)这次抽样调查的学生人数一共有 人;
(2)求频数分布表中 a 的值,并补全频数分布直方图; ,
(3)若该县有 5000 名九年级学生,请你估计全县九年级学生平均每天居家锻炼时间不超过20分钟的有多少人?
时间 x/分 | 人数/人 | 频率 |
0<x≤10 | 102 | 25.5% |
10<x≤20 | 132 | 33% |
20<x≤30 | a | 17.5% |
30<x≤40 | 59 | 14.75% |
40<x≤50 | 29 | 7.25% |
50<x≤60 | 8 | 2% |