题目内容
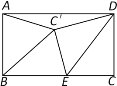
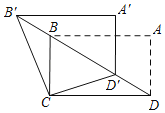
【题目】如图,在矩形ABCD中,AB=![]() ,BC=1,将△ABD沿射线DB平移得到△A'B'D',连接B′C,D′C,则B'C+D'C的最小值是_____.
,BC=1,将△ABD沿射线DB平移得到△A'B'D',连接B′C,D′C,则B'C+D'C的最小值是_____.
【答案】![]()
【解析】
根据矩形的性质和勾股定理可得BD=2,即为B′D′的长,作点C关于BD的对称点G,连接CG交BD于E,连接D′G,如图,则有CD′=GD′,CE⊥BD,CG=2CE,利用三角形的面积可求得CG=![]() ,然后以B′D′,GD′为邻边作平行四边形B′D′GH,可得B′H=D′G=CD′,于是当C,B′,H在同一条直线上时,CB′+B′H最短,且B'C+D'C的最小值=CH,再根据勾股定理即可求出结果.
,然后以B′D′,GD′为邻边作平行四边形B′D′GH,可得B′H=D′G=CD′,于是当C,B′,H在同一条直线上时,CB′+B′H最短,且B'C+D'C的最小值=CH,再根据勾股定理即可求出结果.
解:∵四边形ABCD是矩形,
∴AD=BC=1,∠A=90°,
∴![]() ,
,
∵将△ABD沿射线DB平移得到△A'B'D',
∴B′D′=BD=2,
作点C关于BD的对称点G,连接CG交BD于E,连接D′G,如图,

则CD′=GD′,CE⊥BD,CG=2CE,
∵CE=![]() ,∴CG=
,∴CG=![]() ,
,
以B′D′,GD′为邻边作平行四边形B′D′GH,
则B′H=D′G=CD′,
∴当C,B′,H在同一条直线上时,CB′+B′H最短,
则B'C+D'C的最小值=CH,
∵四边形B′D′GH是平行四边形,
∴HG=B′D′=2,HG∥B′D′,
∴HG⊥CG,
∴CH=![]() .
.
故答案为:![]() .
.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目