Question

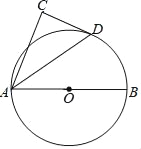
【题目】如图，已知△ABC内接于⊙O，AB是直径，OD∥AC，AD=OC．

（1）当∠B=30°时，请判断四边形OCAD的形状，为什么？

（2）当∠B等于多少度时，AD与⊙O相切？请说明理由．

Answer 1

【答案】（1）菱形，见解析；（2）45°，见解析

【解析】

（1）∠B=∠AOC=30°，得出∠AOC=60°，从而证得OC=OA=AC，则AC=OC，四边形OCAD是菱形；

（2）若AD与⊙O相切，根据切线的性质得出∠OAD=90°，根据AD∥OC，内错角相等得出∠AOC=90°，从而求得∠B=∠AOC=45°．

解：（1）四边形OCAD是菱形．

理由：∵OA=OC，AD=OC，

∴OA=AD，

∴∠OAC=∠OCA，∠AOD=∠ADO，

∵OD∥AC，

∴∠OAC=∠AOD，

∴∠OAC=∠OCA=∠AOD=∠ADO，

∴∠AOC=∠OAD，

∴OC∥AD，

∴四边形OCAD是平行四边形，

∵∠B=30°，

∴∠AOC=60°，

∴OC=OA=AC，

∴AC=OC，

∴四边形OCAD是菱形．

（2）∵AD与⊙O相切，

∴∠OAD=90°，

∵AD∥OC，

∴∠AOC=90°，

∴∠B=∠AOC=45°．