Question

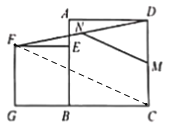
【题目】如图，已知点E在正方形ABCD的边AB上，以BE为边向正方形ABCD外部作正方形BEFG，连接DF，M、N分别是DC、DF的中点，连接MN.若AB=7，BE=5，则MN=_______.

Answer 1

【答案】

【解析】

连接FC，根据三角形中位线定理可得FC=2MN，继而根据四边形ABCD，四边形EFGB是正方形，推导得出G、B、C三点共线，然后再根据勾股定理可求得FC的长，继而可求得答案.

连接FC，∵M、N分别是DC、DF的中点，

∴FC=2MN，

∵四边形ABCD，四边形EFGB是正方形，

∴∠FGB=90°，∠ABG=∠ABC=90°，FG=BE=5，BC=AB=7，

∴∠GBC=∠ABG+∠ABC=180°，

即G、B、C三点共线，

∴GC=GB+BC=5+7=12，

∴FC==13，

∴MN=，

故答案为：.