题目内容
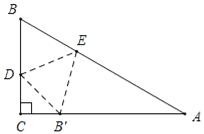
【题目】在Rt△ABC中,∠C=90°,∠A=30°,AB=6,点D,E分别是BC,AB上的动点,将△BDE沿直线DE翻折,点B的对应点B′恰好落在AC上,若△AEB′是等腰三角形,那么CB′的值是________________.
【答案】3或3![]() -3或0
-3或0
【解析】
分三种情况讨论:当AB'=EB'时,△AEB′是等腰三角形;当AE=AB'时,△AEB′是等腰三角形;当AE=B'E时,△AEB′是等腰三角形,分别根据等腰三角形的性质以及勾股定理进行计算,即可得到CB′的值.
解:∵∠C=90°,∠A=30°,AB=6,
∴∠B=60°,BC=3,
分三种情况讨论:
①如图所示,当点D与点C重合时,∠B=∠CB'E=60°,
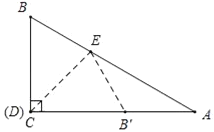
∵∠A=30°,
∴∠AEB'=30°,
∴∠A=∠AEB',
∴AB'=EB',即△AEB′是等腰三角形,
此时,CB'=BC=3;
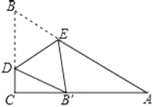
②如图所示,当AE=AB'时,△AEB′是等腰三角形,
∴∠AB'E=75°,
由折叠可得,∠DB'E=∠ABC=60°,
∴∠DB'C=45°,
又∵∠C=90°,
∴△DCB'是等腰直角三角形,
设CB'=x=DC,则BD=3﹣x=DB',
∵Rt△DCB'中,x2+x2=(3﹣x)2,
解得x1=3![]() ﹣3,x2=﹣3
﹣3,x2=﹣3![]() ﹣3(舍去),
﹣3(舍去),
∴CB'=3![]() ﹣3;
﹣3;
③如图所示,当点B'与点C重合时,∠B=∠DCE=60°,

∴∠EB'A=30°=∠A,
∴AE=B'E,即△AEB′是等腰三角形,
此时CB'=0,
综上所述,当△AEB′是等腰三角形时,CB′的值是3或3![]() ﹣3或0.
﹣3或0.
故答案为:3或3![]() -3或0.
-3或0.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目