题目内容
【题目】（本题满分6分）如图，CD∥AF，∠CDE=∠BAF，AB⊥BC，∠C=140°，∠E=80°，试求∠F的度数．
【答案】150°．
【解析】
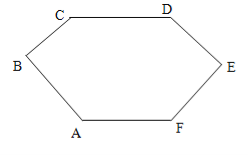
试题分析：过E作EG∥CD，可得到∠CDE+∠DEF+F=360°，再结合多边形的内角和及已知条件，可求得∠F．
试题解析：如图，过E作EG∥CD，∵CD∥AF，∴EG∥AF，∴∠CDE+∠DEG=∠F+∠FGE=180°，∴∠CDE+∠DEG+∠FGE+∠F=360°，又∵∠DEF=80°，∴∠CDE+∠F=360°﹣80°=280°①，又∵∠BAF+∠B+∠C+∠CDE+∠DEF+∠F=（6﹣2）×180°=720°，∵AB⊥BC，∠C=140°，∠CDE=∠BAF，∴90°+140°+80°+2∠CDE+∠F=720°，∴2∠CDE+∠F=390°②，由①②可求得∠F=150°．
练习册系列答案
小学教材全测系列答案
相关题目
