题目内容
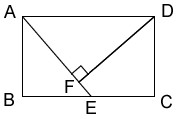
(本题满分8分)如图,在矩形ABCD中,AB=3cm,AD=4cm,点E是BC上一动点(不与B、C重合),且DF⊥AE,垂足为F. 设AE=xcm,DF=ycm.
小题1:(1)求证:△DFA∽△ABE;(4分)
小题2:(2)试求y与x之间的函数关系式,并求出自变量的取值范围. (4分)
小题1:(1)求证:△DFA∽△ABE;(4分)
小题2:(2)试求y与x之间的函数关系式,并求出自变量的取值范围. (4分)


小题1:(1)略;(4分)
小题2:(2)

(1)要求△ABE∽△DFA,能看出有一对直角相等,只需要再找一对角相等,因为四边形ABCD是长方形,那么就出现平行线,有线的平行可得出一对内错角相等,故可证两三角形相似.
(2)由(1)的相似,可得到比例线段,就可得出x与y的关系式,通过观察图可以知道,AE最小大于AB,最大小于AC,再由勾股定理可求出AC的值,因此可得x的取值范围.
解:(1)∵四边形ABCD是长方形,
∴AD∥BC,∠ABE=90°.
∴∠DAF=∠AEB.
又∵DF⊥AE,
∴∠AFD=90°.
∴∠ABE=∠DFA.
∴△ABE∽△DFA.
(2)∵△ABE∽△DFA,
∴ .
.
∴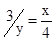 .
.
∴xy=12.
∴y=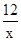 .
.
根据图可知,AE最小大于AB,最大小于AC,AC=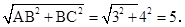
∴3<x<5.
(2)由(1)的相似,可得到比例线段,就可得出x与y的关系式,通过观察图可以知道,AE最小大于AB,最大小于AC,再由勾股定理可求出AC的值,因此可得x的取值范围.
解:(1)∵四边形ABCD是长方形,
∴AD∥BC,∠ABE=90°.
∴∠DAF=∠AEB.
又∵DF⊥AE,
∴∠AFD=90°.
∴∠ABE=∠DFA.
∴△ABE∽△DFA.
(2)∵△ABE∽△DFA,
∴
 .
.∴
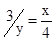 .
.∴xy=12.
∴y=
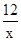 .
.根据图可知,AE最小大于AB,最大小于AC,AC=
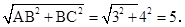
∴3<x<5.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 ,则它的两条对角线的长分别为___________
,则它的两条对角线的长分别为___________
 中,
中,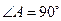 ,
, ,
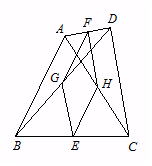
, ,另有一等腰梯形
,另有一等腰梯形 (
( )的底边
)的底边 与
与 重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.
重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.
 ,将等腰梯形
,将等腰梯形 与点
与点 重合时停止.设运动时间为
重合时停止.设运动时间为 秒,运动后的等腰梯形为
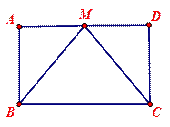
秒,运动后的等腰梯形为 (如图2).
(如图2).
 能否是菱形?若能,请求出此时
能否是菱形?若能,请求出此时 ,求
,求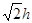 。
。