题目内容
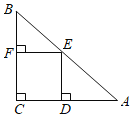
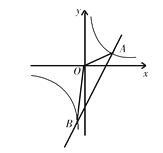
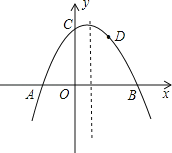
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
(1)求抛物线的解析式;
(2)点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.
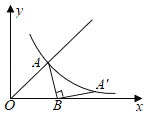
(3)连接AD并延长,过抛物线上一点Q(Q不与A重合)作QN⊥x轴,垂足为N,与射线交于点M,使得QM=3MN,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+3;(2)存在,理由见解析;(3)见解析.
x+3;(2)存在,理由见解析;(3)见解析.
【解析】
(1)点A、C的坐标分别为:(-2,0)、(0,3),将点A、C的坐标代入抛物线表达式,即可求解;
(2)作点D关于对称轴的对称轴D′(-1,2),连接BD′交抛物线对称轴与点P,则点P为所求,即可求解;
(3)QM=|-![]() m2+
m2+![]() m+3-
m+3-![]() m-1|=|-
m-1|=|-![]() m2+2|,3MN=3(
m2+2|,3MN=3(![]() m+1),QM=3MN,即|-
m+1),QM=3MN,即|-![]() m2+2|=3(
m2+2|=3(![]() m+1),即可求解.
m+1),即可求解.
解:(1)点A、C的坐标分别为:(﹣2,0)、(0,3),
将点A、C的坐标代入抛物线表达式得: ,解得:
,解得:![]() ,
,
故抛物线的表达式为:y=﹣![]() x2+
x2+![]() x+3;
x+3;
(2)存在,理由:
作点D关于对称轴的对称轴D′(﹣1,2),连接BD′交抛物线对称轴与点P,则点P为所求,
将点B、D′的坐标代入一次函数表达式:y=kx+b并解得:
直线BD′的函数表达式为:y=﹣![]() x+
x+![]() ,
,
抛物线的对称轴为:x=![]() ,当x=
,当x=![]() 时,y=
时,y=![]() ,
,
故点P(![]() ,
,![]() );
);
(3)设点N(m,0),则点M、Q的坐标分别为:(m,![]() m+1)、(m,﹣
m+1)、(m,﹣![]() m2+
m2+![]() m+3),
m+3),

则QM=|﹣![]() m2+
m2+![]() m+3﹣
m+3﹣![]() m﹣1|=|﹣
m﹣1|=|﹣![]() m2+2|,
m2+2|,
3MN=3(![]() m+1),
m+1),
∵QM=3MN,即|﹣![]() m2+2|=3(
m2+2|=3(![]() m+1),
m+1),
解得:m=﹣2或﹣1或5,
故点Q(﹣2,3)或(﹣1,2)或(5,﹣7).

【题目】某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
商品 | 甲 | 乙 |
进价(元/件) |
|
|
售价(元/件) | 200 | 100 |
若用360元购进甲种商品的件数与用180元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价是多少元?
(2)若超市销售甲、乙两种商品共50件,其中销售甲种商品为![]() 件(
件(![]() ),设销售完50件甲、乙两种商品的总利润为
),设销售完50件甲、乙两种商品的总利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式,并求出
之间的函数关系式,并求出![]() 的最小值.
的最小值.