题目内容
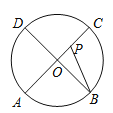
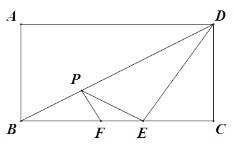
【题目】如图,已知:在矩形ABCD中,AB=2,BC=4,P是对角线BD上的一个动点,作PF⊥BD于P,交边BC于点F(点F与点B、C都不重合),E是射线FC上一动点,连接PE、ED,并一直保持∠EPF=∠FBP,设B、P两点的距离为x,△DEP的面积为y
(1)求出tan∠PBF;
(2)求y关于x的函数解析式,并写出自变量的取值范围
(3)当△DEP与△BCD相似时,求△DEP的面积
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当∠DEP=90°时,面积为
;(3)当∠DEP=90°时,面积为![]() ;当∠PDE=90°时,面积为
;当∠PDE=90°时,面积为![]()
【解析】
(1)利用矩形的性质以及锐角三角函数关系进而得出![]() ,即可得出tan∠PBF的值;
,即可得出tan∠PBF的值;
(2)首先根据相似三角形的判定定理得出![]() ,然后利用相似三角形的性质进而得出
,然后利用相似三角形的性质进而得出![]() ,即可求出y与x的函数关系;
,即可求出y与x的函数关系;
(3)利用当△DEP与△BCD相似时,只有两种情况:∠DEP=∠C=90°或∠EDP=∠C=90°,分别利用勾股定理和相似三角形的性质计算得出答案即可.
(1)∵四边形ABCD是矩形,
![]()
![]()
又![]()
![]()
![]() 即
即![]()
又![]()
![]()
![]()
![]() ,即
,即![]()

如图,作![]() 垂足为H,则
垂足为H,则![]()
又![]()
![]()
![]()
设![]() 则
则![]() ,
,
![]() ,
,
又![]()
由勾股定理得:
![]()
![]() =
=![]()
![]()
又![]()
![]()
当△DEP与△BCD相似时,
只有两种情况:∠DEP=∠C=90°或∠EDP=∠C=90°
①当∠DEP=90°,
∵∠DPE+∠PDE=90°即
∠PDE=∠CBD
∴BE=DE
设CE=a,则BE=DE=4-a
在Rt△DEC中,勾股定理得
![]()
解之![]()
则![]() ,
,
又∵△BCD的面积![]() =4
=4

![]()
②当∠EDP=90°,如图2,
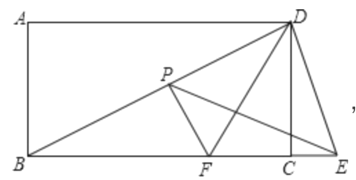
![]()
![]()
![]()
![]()

![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目