题目内容
(本题满分10分)如图(1),点M、N分别是正方形ABCD的边AB、AD的中点,连接CN、DM.
(1)判断CN、DM的数量关系与位置关系,并说明理由;
(2)如图(2),设CN、DM的交点为H,连接BH,求证:△BCH是等腰三角形;
(3)将△ADM沿DM翻折得到△A′DM,延长MA′交DC的延长线于点E,如图(3),求tan∠DEM.


(1)判断CN、DM的数量关系与位置关系,并说明理由;
(2)如图(2),设CN、DM的交点为H,连接BH,求证:△BCH是等腰三角形;
(3)将△ADM沿DM翻折得到△A′DM,延长MA′交DC的延长线于点E,如图(3),求tan∠DEM.



24.(1)CN=DM,CN⊥DM,
证明:∵点M、N分别是正方形ABCD的边AB、AD的中点
∴AM=DN.AD=DC.∠A=∠CDN
∴△AMD≌△DNC,
∴CN=DM.∠CND=∠AMD
∴∠CND+∠NDM=∠AMD+∠NDM=900
∴CN⊥DM
∴CN=DM,CN⊥DM…………………………………………3分
(2)证明:延长DM、CB交于点P.
∵ AD∥BC,∴∠MPC=∠MDA,∠A=∠MBP
∵ MA=MB△AMD≌△BMP,∴ BP=AD=BC.
∵∠CHP=900 ∴BH=BC,即△BCH是等腰三角形……………………6分
(3)∵AB∥DC ∴∠EDM=∠AMD=∠DME ∴EM=ED
设AD=A′D=4k,则A′M=AM=2k,
∴DE=EA′+2k.在Rt△DA′E中,A′D2+A′E2=DE2
∴(4k)2+A′E2=(EA′+2k)2解得A′E=3k,
∴tan∠DEM=A′D:A′E= .………………………………10分
.………………………………10分
证明:∵点M、N分别是正方形ABCD的边AB、AD的中点
∴AM=DN.AD=DC.∠A=∠CDN
∴△AMD≌△DNC,
∴CN=DM.∠CND=∠AMD
∴∠CND+∠NDM=∠AMD+∠NDM=900
∴CN⊥DM
∴CN=DM,CN⊥DM…………………………………………3分
(2)证明:延长DM、CB交于点P.
∵ AD∥BC,∴∠MPC=∠MDA,∠A=∠MBP
∵ MA=MB△AMD≌△BMP,∴ BP=AD=BC.
∵∠CHP=900 ∴BH=BC,即△BCH是等腰三角形……………………6分
(3)∵AB∥DC ∴∠EDM=∠AMD=∠DME ∴EM=ED
设AD=A′D=4k,则A′M=AM=2k,
∴DE=EA′+2k.在Rt△DA′E中,A′D2+A′E2=DE2
∴(4k)2+A′E2=(EA′+2k)2解得A′E=3k,
∴tan∠DEM=A′D:A′E=
 .………………………………10分
.………………………………10分略

练习册系列答案
相关题目
 、
、 、
、 分别是等边
分别是等边 的边BC、CA、AB的中点,在图2中,
的边BC、CA、AB的中点,在图2中, 、
、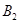 、
、 分别是
分别是 的边
的边 、
、 、
、 的中点,……,按此规律,则第n个图形中菱形的个数共有( )个
的中点,……,按此规律,则第n个图形中菱形的个数共有( )个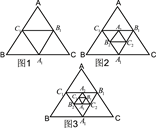
 B.
B.  C.
C.  D.
D. 
 ,若
,若 ,
, ,则梯形ABCD的周长为____▲_____。
,则梯形ABCD的周长为____▲_____。

 折叠后,点
折叠后,点 分别落在
分别落在 的位置.若
的位置.若 ,则
,则 等于_______度.
等于_______度.




 向点D以1 cm/s的速度移动,点Q从点C出发沿CB向点B以2 cm/s的速度移动,若点P、Q分别从点A、C同时出发,设移动时间为t s,则t为何值时,梯形PQCD是等腰梯形?
向点D以1 cm/s的速度移动,点Q从点C出发沿CB向点B以2 cm/s的速度移动,若点P、Q分别从点A、C同时出发,设移动时间为t s,则t为何值时,梯形PQCD是等腰梯形?