题目内容
【题目】等腰三角形中,两腰和底的长分别是10和13,求三角形的三个内角的度数(精确到1′) .
【答案】解:如图所示,AB=AC=10,BC=13,AD是底边上的高,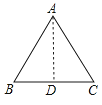
∵AD是底边上的高,
∴AD⊥BC ,
又∵AB=AC ,
∴BD=CD=6.5,∠BAD=∠CAD= ![]() ∠BAC ,
∠BAC ,
在Rt△ABD中,sin∠BAD= ![]() =0.65,
=0.65,
∴∠BAD≈40°32′,
∴∠BAC≈2∠BAD≈81°4′,∠B=∠C≈49°28′ .
故△ABC的三个内角分别为:81°4′,49°28′,49°28′ .
【解析】先画图,AB=AC=10,BC=13,AD是底边上的高,利用等腰三角形三线合一定理可知BD=CD=6.5,∠BAD=∠CAD= ![]() ∠BAC , 在Rt△ABD中,利用∠BAD的正弦值的计算,结合计算器,可求∠BAD , 从而可求∠B、∠BAC , 那么∠C=∠B即可求 .
∠BAC , 在Rt△ABD中,利用∠BAD的正弦值的计算,结合计算器,可求∠BAD , 从而可求∠B、∠BAC , 那么∠C=∠B即可求 .

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目






