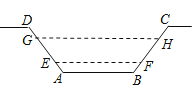
题目内容
【题目】如图①所示,将直尺摆放在三角板上,使直尺与三角板的边分别交于点D , E , F , G , 已知∠CGD=42°
(1)求∠CEF的度数;
(2)将直尺向下平移,使直尺的边缘通过三角板的顶点B , 交AC边于点H , 如图②所示,点H , B在直尺上的度数分别为4,13.4,求BC的长(结果保留两位小数).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
【答案】
(1)
解:∵∠CGD=42°,∠C=90°,
∴∠CDG=90°-42°=48°,
∵DG∥EF,
∴∠CEF=∠CDG=48°;
(2)
解:∵点H,B的读数分别为4,13.4,
∴HB=13.4-4=9.4(m),
∴BC=HBcos42°≈9.4×0.74≈6.96(m).
答:BC的长为6.96m.
【解析】(1)先根据直角三角形的两锐角互为求出∠CDG的度数,再根据两直线平行,同位角相等求出∠DEF , 然后根据三角形的一个外角等于与它不相邻的两个内角的和即可求出∠EFA;(2)根据度数求出HB的长度,再根据∠CBH=∠CGD=42°,利用42°的余弦值进求解.

练习册系列答案
相关题目