题目内容
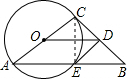
已知:如图,AC是⊙O的直径,AB和⊙O相交于E,BC和⊙O相切于C,D在BC上,DE是⊙O的切线,E 是切点,
是切点,
求证:(1)OD∥AB;
(2)2DE2=BE•OD;
(3)设BE=2,∠ODE=a,则cos2a=
.
 是切点,
是切点,求证:(1)OD∥AB;
(2)2DE2=BE•OD;
(3)设BE=2,∠ODE=a,则cos2a=
| 1 |
| OD |
(1)证明:连接CE,∵DC和DE都与⊙O相切,
∴DC=DE,∠CDO=∠EDO,
∴OD⊥CE.(1分)
又AC是直径,故∠CEA=90°,
即AE⊥CE,
∴OD∥AB;(2分)
(2)证明:
证法一:DE、DC是⊙O的切线,OD∥AB,故∠ODE=∠ODC=∠B.(3分)
∴Rt△BCE∽Rt△DOE,
∴BC:OD=BE:DE,
即BC•DE=OD•BE.(5分)
而DE是Rt△BCE斜边上的中线,故BC=2DE,
∴2DE2=BE•OD.(6分)
证法二:BC2=BE•BA,OD是△ABC的中位线,(3分)
∴BA=2OD,又BC=2DE,
∴4DE2=BE•2OD,
∴2DE2=BE•OD.(6分)
(3)
解法一:由②和已知条件得DE2=OD,即OD2-OE2=OD.(7分)
两边同除以OD2得1-(
)2-
,
得1-sin2a=
,
∴cos2a=
(8分)
解法二:注意到D是BC的中点,可知DB=DE,
∴∠DEB=∠DBE=α,于是cosa=
(过D作DG⊥EB可知).(7分)
由(2)及已知可得DE2=OD,
∴cos2a=
.(8分)
∴DC=DE,∠CDO=∠EDO,
∴OD⊥CE.(1分)
又AC是直径,故∠CEA=90°,
即AE⊥CE,
∴OD∥AB;(2分)
(2)证明:
证法一:DE、DC是⊙O的切线,OD∥AB,故∠ODE=∠ODC=∠B.(3分)
∴Rt△BCE∽Rt△DOE,
∴BC:OD=BE:DE,
即BC•DE=OD•BE.(5分)
而DE是Rt△BCE斜边上的中线,故BC=2DE,
∴2DE2=BE•OD.(6分)
证法二:BC2=BE•BA,OD是△ABC的中位线,(3分)
∴BA=2OD,又BC=2DE,
∴4DE2=BE•2OD,
∴2DE2=BE•OD.(6分)
(3)
解法一:由②和已知条件得DE2=OD,即OD2-OE2=OD.(7分)
两边同除以OD2得1-(
| OE |
| OD |
| 1 |
| OD |
得1-sin2a=
| 1 |
| OD |
∴cos2a=
| 1 |
| OD |
解法二:注意到D是BC的中点,可知DB=DE,
∴∠DEB=∠DBE=α,于是cosa=
| 1 |
| DE |
由(2)及已知可得DE2=OD,
∴cos2a=
| 1 |
| OD |


练习册系列答案
相关题目

 于点D、E,且EF⊥AC,垂足为F,设OB=x,CF=y.
于点D、E,且EF⊥AC,垂足为F,设OB=x,CF=y.
 件表示r.
件表示r.

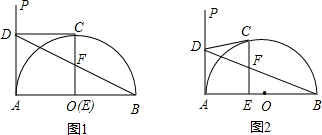 相等关系是否保持不变,并证明你的结论.
相等关系是否保持不变,并证明你的结论.
