题目内容
如图,已知AB是半圆O的直径,AP为过点A的半圆的切线.在
上任取一点C(点C与A、B不重合),过点C作半圆的切线CD交AP于点D;过点C作CE⊥AB,垂足为E.连接BD,交CE于点F.
(1)当点C为
的中点时(如图1),求证:CF=EF;
(2)当点C不是
的中点时(如图2),试判断CF与EF的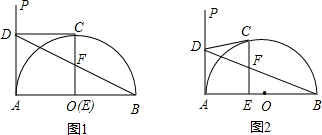 相等关系是否保持不变,并证明你的结论.
相等关系是否保持不变,并证明你的结论.
 |
| AB |
(1)当点C为
 |
| AB |
(2)当点C不是
 |
| AB |
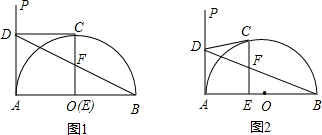 相等关系是否保持不变,并证明你的结论.
相等关系是否保持不变,并证明你的结论.证明:(1)∵DA是切线,AB为直径,
∴DA⊥AB.
∵点C是
的中点,且CE⊥AB,
∴点E为半圆的圆心.
又∵DC是切线,
∴DC⊥EC.
又∵CE⊥AB,
∴四边形DAEC是矩形.
∴CD∥AO,CD=AD.
∴
=
=
.
即EF=
AD=
EC.
∴F为EC的中点,CF=EF.
(2)CF=EF,
证明:连接BC,并延长BC交AP于G点,连接AC,如图所示:
∵AD、DC是半圆O的切线,∴DC=DA,
∴∠DAC=∠DCA.
∵AB是直径,
∴∠ACB=90°,
∴∠ACG=90°.
∴∠DGC+∠DAC=∠DCA+∠DCG=90°.
∴∠DGC=∠DCG.
∴在△GDC中,GD=DC.
∵DC=DA,
∴GD=DA.
∵AP是半圆O的切线,
∴AP⊥AB,又CE⊥AB.
∴CE∥AP.
∴
=
=
.
∵GD=AD,
∴CF=EF.

∴DA⊥AB.
∵点C是
 |
| AB |
∴点E为半圆的圆心.
又∵DC是切线,
∴DC⊥EC.
又∵CE⊥AB,
∴四边形DAEC是矩形.
∴CD∥AO,CD=AD.
∴
| EF |
| AD |
| BE |
| AB |
| 1 |
| 2 |
即EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴F为EC的中点,CF=EF.
(2)CF=EF,
证明:连接BC,并延长BC交AP于G点,连接AC,如图所示:
∵AD、DC是半圆O的切线,∴DC=DA,
∴∠DAC=∠DCA.
∵AB是直径,
∴∠ACB=90°,
∴∠ACG=90°.
∴∠DGC+∠DAC=∠DCA+∠DCG=90°.
∴∠DGC=∠DCG.
∴在△GDC中,GD=DC.
∵DC=DA,
∴GD=DA.
∵AP是半圆O的切线,
∴AP⊥AB,又CE⊥AB.
∴CE∥AP.
∴
| CF |
| GD |
| BE |
| AB |
| EF |
| AD |
∵GD=AD,
∴CF=EF.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



 是切点,
是切点,

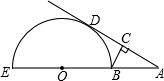
 BM于N,AN的延长线交BC于D,直线AB交⊙A于P,K两点,作MT⊥BC于T.
BM于N,AN的延长线交BC于D,直线AB交⊙A于P,K两点,作MT⊥BC于T.