题目内容
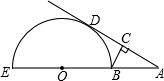
如图①,直线AM⊥AN,⊙O分别与AM、AN相切于B、C两点,连接OC、BC,则有∠ACB=∠OCB;(请思考:为什么?)如果测得AB=a,则可知⊙O的半径r=a.(请思考:为什么?)
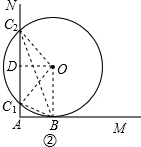
(1)将图①中直线AN向右平移,与⊙O相交于C1、C2两点,⊙O与AM的切点仍记为B,如图②.请你写出与平移前相应的结论,并将图②补充完整;判断此结论是否成立,且说明理由.
(2)在图②中,若只测得AB=a,能否求出⊙O的半径r?若能求出,请你用a表示r;若不能求出,请补充一个条件(补充条件时不能添加辅助线,若补充线段请用b表示,若补充角请用α表示),并用a和补充的条 件表示r.
件表示r.
(1)将图①中直线AN向右平移,与⊙O相交于C1、C2两点,⊙O与AM的切点仍记为B,如图②.请你写出与平移前相应的结论,并将图②补充完整;判断此结论是否成立,且说明理由.
(2)在图②中,若只测得AB=a,能否求出⊙O的半径r?若能求出,请你用a表示r;若不能求出,请补充一个条件(补充条件时不能添加辅助线,若补充线段请用b表示,若补充角请用α表示),并用a和补充的条
 件表示r.
件表示r.(1)图②中相应结论为∠AC1B=∠OC1B和∠AC2B=∠OC2B.(2分)
先证∠AC1B=∠OC1B.
连接OB、OC1,
∵AM与⊙O相切于B,
∴OB⊥AM;
∵AN⊥AM,
∴OB∥AN,
∴∠AC1B=∠OBC1;
∵OB=OC1,
∴∠OBC1=∠OC1B,
∴∠AC1B=∠OC1B.
同理可证∠AC2B=∠OC2B.(4分)
(2)若只测得AB=a,不能求出⊙O的半径r.(5分)
补充条件:另测得AC1=b.(6分)
作OD⊥C1C2,则C1D=C2D.
∵AB2=AC1•AC2,∴AC2=
.
∴C1C2=AC2-AC1=
-b=
.
∴C1D=
C1C2=
.
故r=OB=AD=AC1+C1D=b+
=
.(10分)
说明:1.①若补充条件:另测得AC1=b,则r=
;
②若补充条件:另测得C1C2=b,则r=
;
③若补充条件:另测得BC1=b,则r=
;
④若补充条件:另测得∠ABC1=α,则r=
.
2.以上答案供参考,若有其他答案,只要正确,都应给分.
先证∠AC1B=∠OC1B.
连接OB、OC1,
∵AM与⊙O相切于B,
∴OB⊥AM;
∵AN⊥AM,
∴OB∥AN,
∴∠AC1B=∠OBC1;
∵OB=OC1,
∴∠OBC1=∠OC1B,
∴∠AC1B=∠OC1B.
同理可证∠AC2B=∠OC2B.(4分)
(2)若只测得AB=a,不能求出⊙O的半径r.(5分)
补充条件:另测得AC1=b.(6分)
作OD⊥C1C2,则C1D=C2D.
∵AB2=AC1•AC2,∴AC2=
| a2 |
| b |
∴C1C2=AC2-AC1=
| a2 |
| b |
| a2-b2 |
| b |
∴C1D=
| 1 |
| 2 |
| a2-b2 |
| 2b |
故r=OB=AD=AC1+C1D=b+
| a2-b2 |
| 2b |
| a2+b2 |
| 2b |
说明:1.①若补充条件:另测得AC1=b,则r=
| a2+b2 |
| 2b |
②若补充条件:另测得C1C2=b,则r=
| ||
| 2 |
③若补充条件:另测得BC1=b,则r=
b2
| ||
| 2(b2-a2) |
④若补充条件:另测得∠ABC1=α,则r=
| a |
| 2sinαcosα |
2.以上答案供参考,若有其他答案,只要正确,都应给分.


练习册系列答案
相关题目





 是切点,
是切点,