题目内容
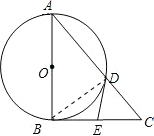
如图，Rt△ABC中，∠ABC=90°，以AB为直径的⊙O交AC于点D，过点D的切线交BC于E．
（1）求证：DE=
BC；
（2）若tanC=
，DE=2，求AD的长．
（1）求证：DE=
| 1 |
| 2 |
（2）若tanC=
| ||
| 2 |
（1）证明：连接BD，
∵AB是直径，∠ABC=90°，
∴BC是⊙O的切线，∠BDC=90°．
∵DE是⊙O的切线，
∴DE=BE（切线长定理）．
∴∠EBD=∠EDB．
又∵∠DCE+∠EBD=∠CDE+∠EDB=90°，
∴∠DCE=∠CDE，
∴DE=CE．
故DE=
BC．
（2）由（1）知，BC=2DE=4．
在Rt△ABC中，AB=BCtanC=4×
=2
，
AC=
=6．
∵∠ADB=∠ABC=90°，∠A=∠A，
∴△ABD∽△ACB．
∴
=
，
∴
=
．
解得AD=
．
∵AB是直径，∠ABC=90°，
∴BC是⊙O的切线，∠BDC=90°．
∵DE是⊙O的切线，
∴DE=BE（切线长定理）．
∴∠EBD=∠EDB．
又∵∠DCE+∠EBD=∠CDE+∠EDB=90°，
∴∠DCE=∠CDE，
∴DE=CE．
故DE=
| 1 |
| 2 |
（2）由（1）知，BC=2DE=4．
在Rt△ABC中，AB=BCtanC=4×
| ||
| 2 |
| 5 |
AC=
| AB2+BC2 |
∵∠ADB=∠ABC=90°，∠A=∠A，
∴△ABD∽△ACB．
∴
| AD |
| AB |
| AB |
| AC |
∴
| AD | ||
2
|
2
| ||
| 6 |
解得AD=
| 10 |
| 3 |
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
是切点，
BM于N，AN的延长线交BC于D，直线AB交⊙A于P，K两点，作MT⊥BC于T．
直线AE与l相交于点D．
