��Ŀ����
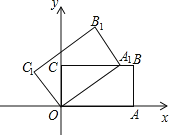
����Ŀ��ij�̳�����һ�ֳɱ�Ϊÿ��60Ԫ��T�����涨�����ڼ����۵��۲����ڳɱ����ۣ��һ������ø���![]() �����������֣�������
�����������֣�������![]() �����������۵���
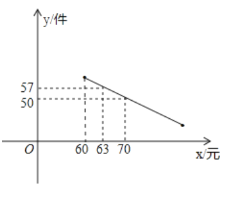
�����������۵���![]() ��Ԫ��֮��ĺ���ͼ����ͼ��ʾ��
��Ԫ��֮��ĺ���ͼ����ͼ��ʾ��
��1����![]() ��
��![]() ֮��ĺ�����ϵʽ����д���Ա���
֮��ĺ�����ϵʽ����д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2�����̳���������T���������Ϊ![]() ��Ԫ�����������
��Ԫ�����������![]() ��Ԫ�������۵���
��Ԫ�������۵���![]() ��Ԫ��֮��ĺ�����ϵʽ������������۵��۶�Ϊ����Ԫʱ���̳��ɻ�����������������Ƕ���Ԫ��
��Ԫ��֮��ĺ�����ϵʽ������������۵��۶�Ϊ����Ԫʱ���̳��ɻ�����������������Ƕ���Ԫ��
���𰸡���1��![]() ��
��![]() ����2��
����2��![]() �������ۼ۶�Ϊ84Ԫ/��ʱ���̳����Ի����������������ʱ864Ԫ��
�������ۼ۶�Ϊ84Ԫ/��ʱ���̳����Ի����������������ʱ864Ԫ��
��������
��1�����ݺ���ͼ��ó��侭����![]() �����ô���ϵ������⼴�ɣ����������۵��۲����ڳɱ����ۣ��һ������ø���
�����ô���ϵ������⼴�ɣ����������۵��۲����ڳɱ����ۣ��һ������ø���![]() ��������Ա���x��ȡֵ��Χ��
��������Ա���x��ȡֵ��Χ��
��2������������![]() �����۵���
�����۵���![]() �ɱ��ۣ�
�ɱ��ۣ�![]() ���������ɵ�
���������ɵ�![]() ��x֮��ĺ�����ϵʽ���ٸ��ݶ��κ�����������⼴�ɵã�
��x֮��ĺ�����ϵʽ���ٸ��ݶ��κ�����������⼴�ɵã�
��1��������ã�����ͼ��Ϊһ�κ������Ҿ�����![]()
��![]() ��
��![]() ֮��ĺ�����ϵʽΪ
֮��ĺ�����ϵʽΪ![]()
��![]()
��ã�![]()
��![]() ��
��![]() ֮��ĺ�����ϵʽΪ
֮��ĺ�����ϵʽΪ![]()
![]()
![]()
��![]() ��
��
��2��![]()
��![]() �������߿�������
�������߿�������
�൱![]() ʱ��
ʱ��![]() ��
��![]() �����������
�����������
�֡�![]()
�൱![]() ʱ��
ʱ��![]() ȡ�����ֵ�����ֵΪ
ȡ�����ֵ�����ֵΪ![]() ��Ԫ��
��Ԫ��
������![]() ��Ԫ�������۵���
��Ԫ�������۵���![]() ��Ԫ��֮��ĺ�����ϵʽΪ
��Ԫ��֮��ĺ�����ϵʽΪ![]() �������ۼ۶�Ϊ84Ԫ/��ʱ���̳����Ի����������������ʱ864Ԫ��
�������ۼ۶�Ϊ84Ԫ/��ʱ���̳����Ի����������������ʱ864Ԫ��

 �����������ҵ�������������ϵ�д�
�����������ҵ�������������ϵ�д� ѧ���������ν��Ͼ���ѧ������ϵ�д�
ѧ���������ν��Ͼ���ѧ������ϵ�д� Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
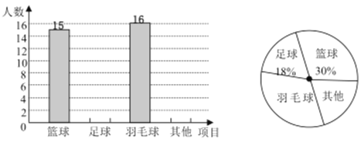
Happy holiday���ּ��������ҵ�㶫���������ϵ�д�����Ŀ��ijУΪ�˽�ȫУѧ�����������Ķ��������Ҫ��ÿ��ѧ���������Ķ�ƪ��������3ƪ�����7ƪ�����������˲���ѧ����ijһ�������Ķ����µ�ƪ�������Ƴ�����ͳ��ͼ����
ijУ����ѧ�������Ķ���ƪ��ͳ�Ʊ�
�����Ķ���ƪ����ƪ�� | 3 | 4 | 5 | 6 | 7 |
�������ˣ� | 20 | 28 |
| 16 | 12 |

�����ͳ��ͼ���е���Ϣ������������⣺
��1������ѧ��������![]() ��ֵ��
��ֵ��
��2���γ���ѧ�������Ķ�ƪ������λ����������
��3������У����800��ѧ�������ݳ���������Ƹ�Уѧ������������
����Ŀ�����κ���![]() Ϊ������
Ϊ������![]() �е�
�е�![]() ��
��![]() �IJ��ֶ�Ӧֵ���±���
�IJ��ֶ�Ӧֵ���±���
x | -1 | 0 | 3 |
y | n | -3 | -3 |
��![]() ʱ�����н�����һ����ȷ����________(����ż���)
ʱ�����н�����һ����ȷ����________(����ż���)
��![]() ���ڵ�
���ڵ�![]() ʱ��
ʱ��![]() ��ֵ��
��ֵ��![]() ֵ�����������
ֵ�����������![]() ���ܵ�
���ܵ�![]() ʱ������
ʱ������![]() ��һԪ���η���
��һԪ���η���![]() �Ľ���
�Ľ���![]() ��
��![]() ��
��