Question

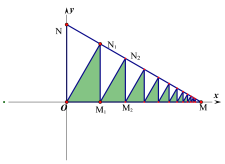
【题目】在平面直角坐标系中，直线与两坐标轴分别交于M、N两点，过点O作，过作，得阴影；再过作，过作，得阴影；……如此进行下去，则得到的所有阴影三角形的面积之和为_________．

Answer 1

【答案】

【解析】

根据相似三角形的性质，相似三角形的面积比等于相似比的平方，那么阴影部分面积与空白部分面积之比为16：25，那么所有的阴影部分面积之和可求了．

解：当x=0时，y=3，

∴ON=3；

当y=0时，，∴x=4，

∴OM=4，

∴MN=5，

∵∠NON1+∠ONN1=90°，∠NON1+∠M1ON1=90°，

∴∠ONN1=∠M1ON1，

∵∠ON1N=∠OM1N1=90°，

∴△ON1N∽△OM1N1，

∴相似比为ON1：ON=sin∠ONN1=4：5，

∴S△OM1N1：S△ON1N =16：25，

同理可得到其他三角形之间也是这个情况，

∴所有的阴影部分面积之和应等于=3×4÷2×．

故答案为：．