Question

【题目】二次函数为常数，中的与的部分对应值如下表：

x	-1	0	3
y	n	-3	-3

当时，下列结论中一定正确的是________(填序号即可)

①；②当时，的值随值的增大而增大；③；④当时，关于的一元二次方程的解是，．

Answer 1

【答案】①②④

【解析】

①根据表格数据得到对称轴为，c=-3﹤0，又n﹥0知a﹥0，即可得出答案；

②根据二次函数的性质即可解答；

③根据二次函数的性质，结合图象即可解答；

④利用待定系数法求出a、b、c，代入解一元二次方程即可解答.

由表格数据知，二次函数的对称轴为，且c=-3﹤0，

∵n﹥0，∴a﹥0,

∵对称轴﹥0，

∴b﹤0即 bc﹥0，故①正确;

∵a﹥0，对称轴为，

∴当x﹥时，的值随值的增大而增大，

∴当时，的值随值的增大而增大，

故②正确；

③由对称轴得：b=-3a，

∴

∵当x=-1时，y=n，

∴n=a+3a-3=4a-3，

∴n﹤4a，故③错误；

④当n=1时，将（-1,1），（0，-3），（3，-3）代入函数解析式中，得：

，

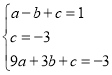解得，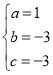

∴关于x的一元二次方程为，解得，，

故④正确，

故答案是：①②④