题目内容
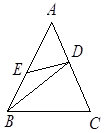
(本题满分12分)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
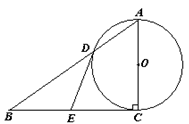
小题1:(1)求证:点E是边BC的中点;(4分)
小题2:(2)若EC=3,BD=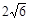 ,求⊙O的直径AC的长度;(4分)
,求⊙O的直径AC的长度;(4分)
小题3:(3)若以点O,D,E,C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由. (4分)

小题1:(1)求证:点E是边BC的中点;(4分)
小题2:(2)若EC=3,BD=
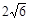 ,求⊙O的直径AC的长度;(4分)
,求⊙O的直径AC的长度;(4分)小题3:(3)若以点O,D,E,C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由. (4分)
小题1:(1)证明:连接DO,
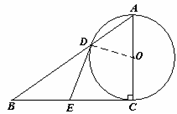
∵∠ACB=90°,AC为直径, ∴EC为⊙O的切线,
又∵ED也为⊙O的切线, ∴EC=ED. (2分)
又∵∠EDO=90°, ∴∠BDE+∠ADO=90°,
∴∠BDE+∠A=90°,
又∵∠B+∠A=90° ∴∠BDE=∠B, ∴EB=ED.
∴EB=EC,即点E是边BC的中点.
小题2:(2)∵BC,BA分别是⊙O的切线和割线,
∴BC2=BD·BA, ∴(2EC)2= BD·BA,即BA·
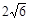 =36,∴BA=
=36,∴BA=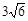 , (6分)
, (6分)在Rt△ABC中,由勾股定理得 AC=
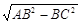 =
=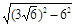 =
=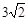 .
.小题3:(3)△ABC是等腰直角三角形. (9分)
理由:∵四边形ODEC为正方形, ∴∠DOC=∠ACB=90°,即DO∥BC,
又∵点E是边BC的中点, ∴BC=2OD=AC,
∴△ABC是等腰直角三角形. (12分)
(1)利用EC为⊙O的切线,ED也为⊙O的切线可求EC=ED,再求得EB=EC,EB=ED可知点E是边BC的中点;
(2)解答此题需要运用圆切线和割线的性质和勾股定理求解;
(3)判定△ABC是等腰直角三角形时要用到正方形的性质来求得相等的边.
(1)证明:连接DO;
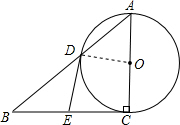
∵∠ACB=90°,AC为直径,
∴EC为⊙O的切线;
又∵ED也为⊙O的切线,
∴EC=ED,
又∵∠EDO=90°,
∴∠BDE+∠ADO=90°,
∴∠BDE+∠A=90°
又∵∠B+∠A=90°,
∴∠BDE=∠B,
∴EB=ED,
∴EB=EC,即点E是边BC的中点;
(2)解:∵BC,BA分别是⊙O的切线和割线,
∴BC2=BD?BA,
∴(2EC)2=BD?BA,即BA?2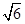 =36,
=36,
∴BA=3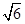 ,
,
在Rt△ABC中,由勾股定理得
AC=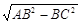 =
=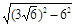 =
=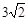 ;
;
(3)解:△ABC是等腰直角三角形.
理由:∵四边形ODEC为正方形,
∴∠DOC=∠ACB=90°,即DO∥BC,
又∵点E是边BC的中点,
∴BC=2OD=AC,
∴△ABC是等腰直角三角形.
(2)解答此题需要运用圆切线和割线的性质和勾股定理求解;
(3)判定△ABC是等腰直角三角形时要用到正方形的性质来求得相等的边.
(1)证明:连接DO;

∵∠ACB=90°,AC为直径,
∴EC为⊙O的切线;
又∵ED也为⊙O的切线,
∴EC=ED,
又∵∠EDO=90°,
∴∠BDE+∠ADO=90°,
∴∠BDE+∠A=90°
又∵∠B+∠A=90°,
∴∠BDE=∠B,
∴EB=ED,
∴EB=EC,即点E是边BC的中点;
(2)解:∵BC,BA分别是⊙O的切线和割线,
∴BC2=BD?BA,
∴(2EC)2=BD?BA,即BA?2
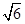 =36,
=36,∴BA=3
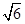 ,
,在Rt△ABC中,由勾股定理得
AC=
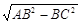 =
=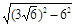 =
=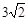 ;
;(3)解:△ABC是等腰直角三角形.
理由:∵四边形ODEC为正方形,
∴∠DOC=∠ACB=90°,即DO∥BC,
又∵点E是边BC的中点,
∴BC=2OD=AC,
∴△ABC是等腰直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
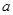 、
、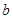 相交于点O,若∠1=50°,则∠2= °.
相交于点O,若∠1=50°,则∠2= °.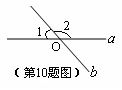
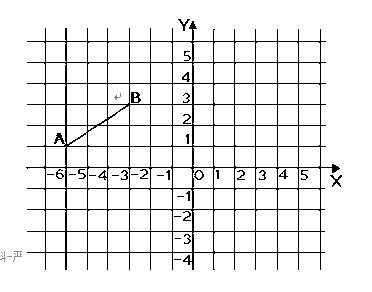


 外一点,点A、B、C为直线
外一点,点A、B、C为直线