题目内容
已知∠AOB=90°，OM是∠AOB的平分线，将三角板的直角顶点P放在射线OM上滑动，两直角边分别与OA、OB交于C、D，PC和PD有怎样的数量关系，证明你的结论。
解：PC=PD
证明：作PE⊥OA,PF⊥OB,垂足分别为E、F。
则有 ∠EC=∠PFD=90°
即 ∠PEO=∠PFD=90°
∵OM平分∠AOB
∴∠POE=∠POF
于是 在△PEO和△PFO中
∵
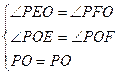
∴ △ PEO≌△PFO(AAS) ……………………6分
∴ PE=PF(全等三角形的对应边相等)
∵ ∠CPD="90" ° 即 ∠CPE+∠EPD=90°
易知∠ EPD="90" ° 即∠ DPF+∠EPF=90°
∴ ∠CPE=∠DPF
于是 在△PEC和△PFD中
∵
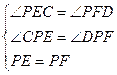
∴ △PEC≌△PFD(AAS)
∴ PC=PD(全等三角形的对应边相等) ………14分
证明：作PE⊥OA,PF⊥OB,垂足分别为E、F。
则有 ∠EC=∠PFD=90°
即 ∠PEO=∠PFD=90°
∵OM平分∠AOB
∴∠POE=∠POF
于是 在△PEO和△PFO中
∵
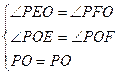
∴ △ PEO≌△PFO(AAS) ……………………6分
∴ PE=PF(全等三角形的对应边相等)
∵ ∠CPD="90" ° 即 ∠CPE+∠EPD=90°
易知∠ EPD="90" ° 即∠ DPF+∠EPF=90°
∴ ∠CPE=∠DPF
于是 在△PEC和△PFD中
∵
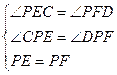
∴ △PEC≌△PFD(AAS)
∴ PC=PD(全等三角形的对应边相等) ………14分
略
练习册系列答案
阅读快车系列答案
相关题目
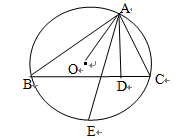
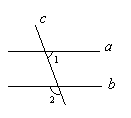
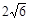，求⊙O的直径AC的长度；（4分）
，
，
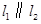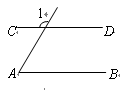
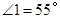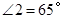,则∠3为（ ）
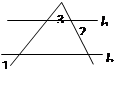
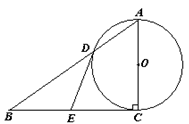
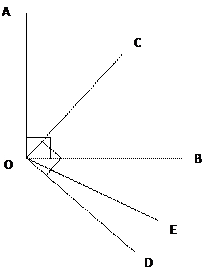试求 ∠COE的度数。