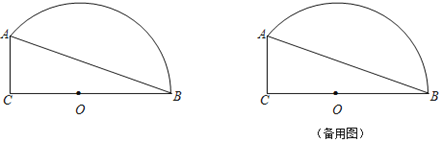题目内容
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() .将矩形沿
.将矩形沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边中点
边中点![]() 处,点
处,点![]() 落在
落在![]() 处.连接
处.连接![]() ,以矩形对称中心
,以矩形对称中心![]() 为圆心的圆与
为圆心的圆与![]() 相切于点
相切于点![]() ,则圆的半径为________.
,则圆的半径为________.
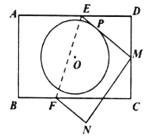
【答案】![]()
【解析】
连接OP、OM、AC,根据矩形的性质、折叠的性质和勾股定理即可求出EM=5,ED=4,然后根据三角形中位线的性质和切线的性质可得OM∥AD,OM=![]() ,∠OPM=∠D=90°,从而证出△OMP∽△MED,最后列出比例式即可求出结论.
,∠OPM=∠D=90°,从而证出△OMP∽△MED,最后列出比例式即可求出结论.
解:连接OP、OM、AC
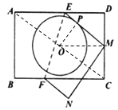
∵矩形![]() 中,
中,![]() ,
,![]() ,点M为CD的中点
,点M为CD的中点
∴∠D=90°,CD=AB=6,AD=BC=9,DM=![]()
由折叠的性质可得AE=EM,设AE=EM=x,则ED=AD-AE=9-x
∵ED2+DM2=EM2
∴(9-x)2+32=x2
解得:x=5
∴EM=5,ED=4
∵以矩形对称中心![]() 为圆心的圆与
为圆心的圆与![]() 相切于点
相切于点![]() ,点M为CD的中点
,点M为CD的中点
∴AC必过点O且OM为△ACD的中位线,OP⊥EM
∴OM∥AD,OM=![]() ,∠OPM=∠D=90°
,∠OPM=∠D=90°
∴∠OMP=∠MED
∴△OMP∽△MED
∴![]()
即![]()
解得:![]()
即圆的半径为![]()
故答案为:![]() .
.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目