题目内容
【题目】已知y关于x的二次函数y=x-bx+![]() b+b-5的图象与x轴有两个公共点.
b+b-5的图象与x轴有两个公共点.
(1)求b的取值范围;
(2)若b取满足条件的最大整数值,当m≤x≤![]() 时,函数y的取值范围是n≤y≤6-2m,求m,n的值;
时,函数y的取值范围是n≤y≤6-2m,求m,n的值;
(3)若在自变量x的值满足b≤x≤b+3的情况下,对应函数y的最小值为![]() ,求此时二次函数的解析式.
,求此时二次函数的解析式.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)利用![]() 即可求解;
即可求解;
(2)根据(1)中的结论确定b的值,进而确定二次函数的表达式,然后根据![]() 与对称轴的位置关系,判断出函数的单调性,然后代入到二次函数解析式中即可求出m,n的值;
与对称轴的位置关系,判断出函数的单调性,然后代入到二次函数解析式中即可求出m,n的值;
(3)根据![]() 与对称轴的位置关系,分三种情况:①当
与对称轴的位置关系,分三种情况:①当![]() ,②当
,②当![]() ,取值范围在对称轴左侧,③当
,取值范围在对称轴左侧,③当![]() ,即
,即![]() 时,取值范围在对称轴右侧,数形结合进行讨论即可.
时,取值范围在对称轴右侧,数形结合进行讨论即可.
解:(1)由题意知,![]()
即![]() ,
,
∴![]()
解得:![]() ;
;
(2)由题意,b=4,代入得:![]() ,
,
∴对称轴为直线![]() .
.
又∵a=1>0,函数图象开口向上,
∴当![]() 时,y随x的增大而减小,
时,y随x的增大而减小,
∴当x=![]() 时,
时,![]() ,
,
当x=m时,y=![]() ,
,
解得:![]() (不合题意,舍去);
(不合题意,舍去);
∴![]() .
.
(3) ![]() ,函数大致图象如图所示.
,函数大致图象如图所示.
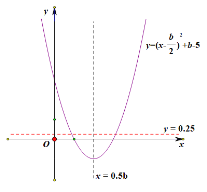
①当![]() ,即
,即![]() 时,
时,
函数y在顶点处取得最小值,有b-5=![]() ,
,
∴b=![]() (不合题意,舍去)
(不合题意,舍去)
②当![]() ,即
,即![]() 时,
时,
取值范围在对称轴左侧,y随x的增大而减小,
∴当x=b+3时,y最小值=![]() ,代入得
,代入得
![]() ,
,
即![]() ,
,
解得:![]() (不合题意,舍去),
(不合题意,舍去),
∴此时二次函数的解析式为:![]()
③当![]() ,即
,即![]() 时,取值范围在对称轴右侧,y随x的增大而增大,
时,取值范围在对称轴右侧,y随x的增大而增大,
∴当x=b时,y最小值=![]() ,代入得
,代入得
![]() ,
,
即![]() ,
,
解得:![]() ,
,
∴此时二次函数的解析式为:![]() .
.
综上所述,符合题意的二次函数的解析式为:![]() 或
或![]()

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目