题目内容
【题目】图1是一辆吊车的实物图,图2是其工作示意图,![]() 是可以伸缩的起重臂,其转动点
是可以伸缩的起重臂,其转动点![]() 离地面
离地面![]() 的高度
的高度![]() 为
为![]() .当起重臂
.当起重臂![]() 长度为
长度为![]() ,张角
,张角![]() 为118°.
为118°.
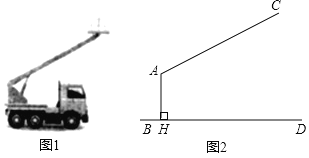
(1)求操作平台![]() 离地面的高度;
离地面的高度;
(2)当张角![]() 为120°,其它条件不变时,求操作平台
为120°,其它条件不变时,求操作平台![]() 升高的高度.
升高的高度.
(最后结果精确到0.1,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
【答案】(1)操作平台C离地面的高度为7.6m;(2)操作平台![]() 升高的高度为0.3m.
升高的高度为0.3m.
【解析】
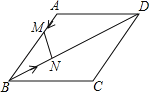
(1)作CE⊥BD于E,AF⊥CE于F,如图2,易得四边形AHEF为矩形,则EF=AH=3.5m,∠HAF=90°,再计算出∠CAF=28°,则在Rt△ACF中利用正弦可计算出CF,然后计算CF+EF即可;
(2)作GQ⊥BD,垂足为Q,交AF于点P,求出GP的长,即可求出GQ的长,然后用GQ-CE即可得到答案.
(1)解:作CE⊥BD于E,AF⊥CE于F,如图,
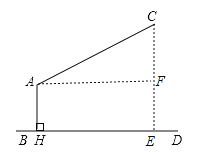
易得四边形AHEF为矩形,
∴EF=AH=3.4m,∠HAF=90°,
∴∠CAF=∠CAH-∠HAF=118°-90°=28°,
在Rt△ACF中,∵sin∠CAF=![]() ,
,
∴CF=9sin28°=9×0.47=4.23,
∴CE=CF+EF=4.23+3.4≈7.6(m),
答:操作平台C离地面的高度为7.6m.
(2)如图,作GQ⊥BD,垂足为Q,交AF于点P,易知PQ=3.4m,
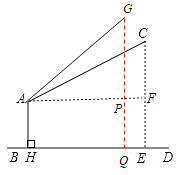
由(1)知,∠HAF=90°,AG=AC=9m,
∴∠GAF=∠GAH-∠HAF=120°-90°=30°,
在Rt△AGP中,∵sin∠GAP=![]() ,
,
∴GP=9sin30°=9×0.5=4.5,
∴GQ=GP+PQ=4.5+3.4=7.9m,
∴操作平台![]() 升高的高度为:GQ-CE=7.9-7.6=0.3m.
升高的高度为:GQ-CE=7.9-7.6=0.3m.

 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案【题目】表中所列![]() 、
、![]() 的7对值是二次函数
的7对值是二次函数![]() 图象上的点所对应的坐标,其中
图象上的点所对应的坐标,其中![]()
| … |
|
|
|
|
|
|
| … |
| … | 6 |
| 11 |
| 11 |
| 6 | … |
根据表中提供约信息,有以下4个判断:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 的值是
的值是![]() ;④
;④![]() ;其中判断正确的是( )
;其中判断正确的是( )
A.①②③B.①②④C.①③④D.②③④