题目内容
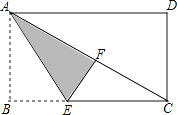
【题目】如图,已知BC是⊙O的弦,A是⊙O外一点,△ABC为正三角形,D为BC的中点,M为⊙O上一点,并且∠BMC=60°.

(1)求证:AB是⊙O的切线;
(2)若E,F分别是边AB,AC上的两个动点,且∠EDF=120°,⊙O的半径为2,试问BE+CF的值是否为定值?若是,求出这个定值;若不是,请说明理由.
【答案】(1)、证明过程见解析;(2)、是定值;定值为![]()
【解析】试题分析:(1)、连结OB、OD、OC,根据D为BC的中点,则OD⊥BC,∠BOD=∠COD,∠ODB=90°,根据∠BMC=![]() ∠BOC得出∠BOD=∠M=60°,则∠OBD=30°,根据△ABC为正三角形得出∠ABC=60°,则∠ABO=90°,即为切线;(2)、作DH⊥AB于H,DN⊥AC于N,连结AD,根据△ABC为正三角形,D为BC的中点则AD平分∠BAC,∠BAC=60°,DH=DN,∠HDN=120°,从而得出△DHE和△DNF全等,则HE=NF,则BE+CF=BH-EH+CN+NF=BH+CN,在Rt△DHB中根据∠DBH=60°得出BH=
∠BOC得出∠BOD=∠M=60°,则∠OBD=30°,根据△ABC为正三角形得出∠ABC=60°,则∠ABO=90°,即为切线;(2)、作DH⊥AB于H,DN⊥AC于N,连结AD,根据△ABC为正三角形,D为BC的中点则AD平分∠BAC,∠BAC=60°,DH=DN,∠HDN=120°,从而得出△DHE和△DNF全等,则HE=NF,则BE+CF=BH-EH+CN+NF=BH+CN,在Rt△DHB中根据∠DBH=60°得出BH=![]() BD,同理得出CN=
BD,同理得出CN=![]() OC,从而得出BE+CF=
OC,从而得出BE+CF=![]() BC,根据BD=OB
BC,根据BD=OB![]() sin30°=
sin30°=![]() 求出BC的长度,从而得出BE+CF为定值
求出BC的长度,从而得出BE+CF为定值![]() .
.
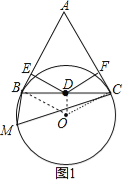
试题解析:(1)、连结OB、OD、OC,如图1, ∵D为BC的中点, ∴OD⊥BC,∠BOD=∠COD,
∴∠ODB=90°, ∵∠BMC=![]() ∠BOC, ∴∠BOD=∠M=60°, ∴∠OBD=30°, ∵△ABC为正三角形,
∠BOC, ∴∠BOD=∠M=60°, ∴∠OBD=30°, ∵△ABC为正三角形,
∴∠ABC=60° ∴∠ABO=60°+30°=90°, ∴AB⊥OB, ∴AB是⊙O的切线;
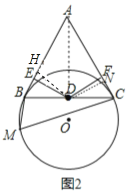
(2)、BE+CF的值是为定值.作DH⊥AB于H,DN⊥AC于N,连结AD,如图2,
∵△ABC为正三角形,D为BC的中点, ∴AD平分∠BAC,∠BAC=60°, ∴DH=DN,∠HDN=120°,
∵∠EDF=120°, ∴∠HDE=∠NDF,在△DHE和△DNF中,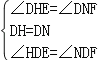 , ∴△DHE≌△DNF,
, ∴△DHE≌△DNF,
∴HE=NF, ∴BE+CF=BH﹣EH+CN+NF=BH+CN, 在Rt△DHB中,∵∠DBH=60°, ∴BH=![]() BD,
BD,
同理可得CN=![]() OC, ∴BE+CF=
OC, ∴BE+CF=![]() OB+
OB+![]() OC=
OC=![]() BC, ∵BD=OB
BC, ∵BD=OB![]() sin30°=
sin30°=![]() , ∴BC=2
, ∴BC=2![]() ,
,
∴BE+CF的值是定值,为![]() .
.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案【题目】已知二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)经过A、B、C、D四个点,其中横坐标x与纵坐标y的对应值如下表:
A | B | C | D | |
x | -1 | 0 | 1 | 3 |
y | -1 | 3 | 5 | 3 |
(1)求二次函数解析式;
(2)求△ABD的面积.