Question

【题目】在中， ， ，点、 分别在射线、上（点不与点、点重合），且保持.

①若点在线段上（如图），且，求线段的长；

②若， ，求与之间的函数关系式，并写出自变量的取值范围；

Answer 1

【答案】（1）；（2），（0＜x＜8）； （x≥8）

【解析】试题分析：（1）求线段CQ的长，根据已知条件AB=AC，∠APQ=∠ABC知道，可以先证明△QCP∽△PBA，由比例关系式得出；

（2）要求y与x之间的函数关系式，以及函数的定义域，需要分两种情况进行讨论：BP在线段CB上，或在CB的延长线上，根据实际情况证明△QCP∽△ABP，根据相似三角形的性质求出比例式，进而得出y与x之间的函数关系式.

解：（1）∵∠APQ+∠CPQ=∠B+∠BAP，∠APQ=∠ABC，

∴∠BAP=∠CQP．

又∵AB=AC，∴∠B=∠C．

∴△CPQ∽△BAP．

∴．

∵AB=AC=5，BC=8，BP=6，CP=8﹣6=2，

∴， ．

(2）若点P在线段CB上，由（1）知，

∵BP=x，BC=8，∴CP=BC﹣BP=8﹣x，

又∵CQ=y，AB=5，∴，即．

故所求的函数关系式为，（0＜x＜8）．

若点P在线段CB的延长线上，如图．

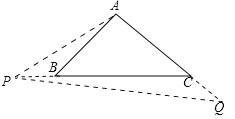
∵∠APQ=∠APB+∠CPQ，

∠ABC=∠APB+∠PAB，∠APQ=∠ABC，

∴∠CPQ=∠PAB．

又∵∠ABP=180°﹣∠ABC，∠PCQ=180°﹣∠ACB，∠ABC=∠ACB，

∴∠ABP=∠PCQ．∴△QCP∽△PBA．∴．

∵BP=x，CP=BC+BP=8+x，AB=5，CQ=y，

∴，即（x≥8）．