题目内容
【题目】如图,长方形纸片ABCD中,已知AD=8,AB=6,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,则CE的长为 . 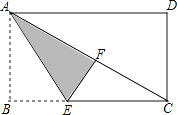
【答案】5
【解析】解:如图,
∵四边形ABCD为矩形,
∴∠D=90°,DC=AB=6;
由勾股定理得:
AC2=AD2+DC2 , 而AD=8,
∴AC=10;由题意得:
∠AFE=∠B=90°,
AF=AB=6;EF=EB(设为λ),
∴CF=10﹣6=4,CE=8﹣λ;
由勾股定理得:
(8﹣λ)2=λ2+42 , 解得:λ=3,
∴CE=5,
故答案为5.
该题主要考查了翻折变换的性质、勾股定理等几何知识点及其应用问题;解题的关键是灵活运用翻折变换的性质、勾股定理等几何知识点来分析、判断、推理或解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】为了了解大气污染情况,某学校兴趣小组搜集了2017年上半年中120天郑州市的空气质量指数,绘制了如下不完整的统计图表:
空气质量指数统计表
级别 | 指数 | 天数 | 百分比 |
优 | 0﹣50 | 24 | m |
良 | 51﹣100 | a | 40% |
轻度污染 | 101﹣150 | 18 | 15% |
中度污染 | 151﹣200 | 15 | 12.5% |
重度污染 | 201﹣300 | 9 | 7.5% |
严重污染 | 大于300 | 6 | 5% |
合计 | 120 | 100% |
请根据图表中提供的信息,解答下面的问题:
(1)空气质量指数统计表中的a= ,m= ;
(2)请把空气质量指数条形统计图补充完整:
(3)若绘制“空气质量指数扇形统计图”,级别为“优”所对应扇形的圆心角是 度;
(4)请通过计算估计郑州市2017年中空气质量指数大于100的天数.