题目内容
【题目】如图,PA,PB是⊙O的两条切线,切点分别为A,B,OP交AB于点C,OP=13,sin∠APC=![]() .
.
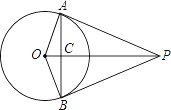
(1)求⊙O的半径;
(2)求弦AB的长.
【答案】(1)半径为5;(2)AB=![]() .
.
【解析】
(1)由题意可推出OA⊥AP,即可推出OA的长度,即半径的长度;
(2)根据题意和(1)的结论,即可推出PA=PB,∠APO=∠BPO,AC=BC=![]() AB,可以推出AC的长度,即可推出AB的长度.
AB,可以推出AC的长度,即可推出AB的长度.
(1)解:∵PA,PB是⊙O的两条切线,
∴∠OAP=90°,
∵sin∠APC= ![]() =
= ![]() ,OP=13,
,OP=13,
∴OA=5,
即所求半径为5
(2)解:Rt△OAP中,AP=12,
∵PA,PB是⊙O的两条切线,
∴PA=PB,∠APO=∠BPO,
∴PC⊥AB
由S四边形OAPB=S△OAP+S△OBP,得![]() OP×AB=OA×AP,
OP×AB=OA×AP,
∴AB=![]() =
=![]()

练习册系列答案
相关题目