题目内容
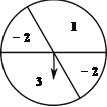
【题目】如图，可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域，其中标有数字“1”的扇形圆心角为120°．转动转盘，待转盘自动停止后，指针指向一个扇形的内部，则该扇形内的数字即为转出的数字，此时，称为转动转盘一次（若指针指向两个扇形的交线，则不计转动的次数，重新转动转盘，直到指针指向一个扇形的内部为止）
(1)转动转盘一次，求转出的数字是－2的概率；
(2)转动转盘两次，用树状图或列表法求这两次分别转出的数字之积为正数的概率．
【答案】（1）
；（2）
.
【解析】（1）根据题意可求得2个“－2”所占的扇形圆心角的度数，再利用概率公式进行计算即可得；
（2）由题意可得转出“1”、“3”、“－2”的概率相同，然后列表得到所有可能的情况，再找出符合条件的可能性，根据概率公式进行计算即可得.
（1）由题意可知：“1”和“3”所占的扇形圆心角为120°，
所以2个“－2”所占的扇形圆心角为360°－2×120°＝120°，
∴转动转盘一次，求转出的数字是－2的概率为
＝；
（2）由（1）可知，该转盘转出“1”、“3”、“－2”的概率相同，均为，所有可能性如下表所示：
第一次 第二次 | 1 | －2 | 3 |
1 | (1，1) | (1，－2) | (1，3) |
－2 | (－2，1) | (－2，－2) | (－2，3) |
3 | (3，1) | (3，－2) | (3，3) |
由上表可知：所有可能的结果共9种，其中数字之积为正数的的有5种，其概率为.
【题目】某人去年水果批发市场采购苹果，他看中了
、
两家苹果．这两家苹果品质一样，零售价都为6元/千克，批发价各不相同．
（1）家规定：批发数量不超过1000千克，按零售价的92%优惠；批发数量超过1000千克且不超过2000千克，所有苹果按零售价的90%优惠；超过2000千克，所有苹果按零售价的88%优惠．
家的规定如下表：
数量范围（千克） | 0—500 | 500以上—1500 | 1500以上—2500 | 2500以上 |
价格（元） | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
表格说明：批发价格分段计算，如某人批发苹果2100千克，则总费用=6×95%×500+6×85%×1000+6×75%×（2100-1500）．
（1）如果他批发600千克苹果，那么他在、两家批发分别需要多少元？
（2）如果他批发
千克苹果（1500<<2000），请你分别用含的代数式表示在、两家批发所需的费用．
（3）现在他要批发1800千克苹果，选择在哪家批发更优惠呢？请说明理由．
