Question

【题目】如图．已知A、B两点的坐标分别为A(0，)，B(2，0)．直线AB与反比例函数的图象交于点C和点D(1，a)．

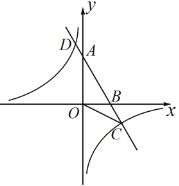
（1）求直线AB和反比例函数的解析式．

（2）求∠ACO的度数．

Answer 1

【答案】（1）y=x+ ，y=﹣；（2）∠ACO=30°；

【解析】

（1）根据A、B两点坐标求得一次函数解析式，再求得D点的具体坐标，从而求得反比例函数的解析式.

（2）联立函数解析式求得C点坐标，过C点作CH⊥x轴于H，证明为等腰三角形，根据特殊直角三角形求得的度数，从而求得的度数.

解：(1)设直线AB的解析式为： ，

把A(0，)，B(2，0)分别代入，

得，，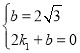

解得 =，b=．

∴直线AB的解析式为：y=x+；

∵点D(1，a)在直线AB上，

∴a=+=，即D点坐标为(1，)，

又∵D点(1，)在反比例函数的图象上，

∴k=1×=﹣，

∴反比例函数的解析式为：y=﹣；

(2)由，解得或，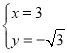

∴C点坐标为(3，﹣)，过C点作CH⊥x轴于H，如图，

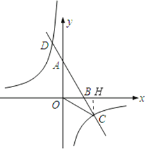
∵OH=3，CH=，

∴OC=，而OA=，

∴OA=OC，

∴∠OAC=∠OCA．

又∵OB=2，

∴AB=，

在Rt△AOB中，

∴∠OAB=30°，

∴∠ACO=30°