题目内容
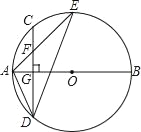
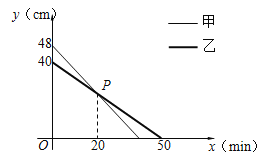
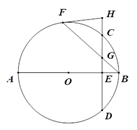
【题目】如图,AB、BF分别是⊙O的直径和弦,弦CD与AB、BF分别相交于点E、G,过点F的切线HF与DC的延长线相交于点H,且HF=HG.
(1)求证:AB⊥CD;
(2)若sin∠HGF=![]() ,BF=3,求⊙O的半径长.
,BF=3,求⊙O的半径长.
【答案】(1)见解析;(2)2
【解析】试题分析:(1)根据切线的性质以及等腰三角形的性质首先求出![]() 进而得出
进而得出![]() ,可得出
,可得出![]()
(2)连接AF,首先得出![]() 利用锐角三角函数得出AB即可得出半径.
利用锐角三角函数得出AB即可得出半径.
试题解析:(1)连接OF.
∵OF=OB,
∴∠OFB=∠B,
∵HF是⊙O的切线,
∴∠OFH=90°
∴∠HFB+∠OFB=90°,
∴∠B+∠HFB=90°,
∵HF=HG,
∴∠HFG=∠HGF,
又∵∠HGF=∠BGE,
∴∠BGE=∠HFG,
∴∠BGE+∠B=90°,
∴∠GEB=90°,
∴AB⊥CD.
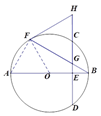
(2)连接AF.
∵AB为⊙O直径,
∴∠AFB=90°,
∴∠A+∠B=90°,
∴∠A=∠BGE,
又∵∠BGE=∠HGF,
∠A=∠HGF,
∵![]()
∵∠AFB=90°,BF=3 ,
∴ AB=4.
∴OA=OB=2 .
即⊙O的半径为2.

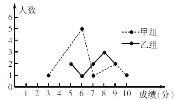
【题目】某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀. 为了解本次大赛的成绩,校团委随机抽取了甲、乙两组学生成绩作为样本进行统计,绘制了如下统计图表:
组别 | 平均数 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.8 | a | 3.76 | 90% | 30% |
乙组 | b | 7.5 | 1.96 | 80% | 20% |
(1)求出表中a,b的值;
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面的表格判断,小英属于哪个组?
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组. 但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.