题目内容
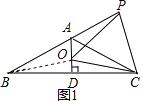
【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,
(1)求∠APO+∠DCO的度数;
(2)求证:AC=AO+AP.

【答案】(1)30°;(2)见解析。
【解析】
(1)利用等边对等角,即可证得:∠APO=∠ABO,∠DCO=∠DBO,则∠APO+∠DCO=∠ABO+∠DBO=∠ABD,据此即可求解;
(2) 在AC上截取AE=PA,先证明△OPA≌△CPE,则AO=CE,AC=AE+CE=AO+AP.
解:(1)如图1,连接OB,
∵AB=AC,AD⊥BC,
∴BD=CD,∠BAD=![]()
∠BAC=×120°=60°,
∴OB=OC,∠ABC=90°-∠BAD=30°
∵OP=OC,
∴OB=OC=OP,
∴∠APO=∠ABO,∠DCO=∠DBO,
∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°;
故答案为:30°;
(2)如图2,在AC上截取AE=PA
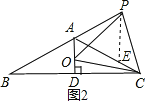 ,
,
∵∠PAE=180°-∠BAC=60°,
∴△APE是等边三角形,
∴∠PEA=∠APE=60°,PE=PA,
∴∠APO+∠OPE=60°,
∵∠OPE+∠CPE=∠CPO=60°,
∴∠APO=∠CPE,
∵OP=CP,
在△OPA和△CPE中,
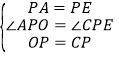
∴△OPA≌△CPE(SAS),
∴AO=CE,
∴AC=AE+CE=AO+AP

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】为了传承优秀传统文化,我市组织了一次初三年级1 200名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:
成绩(分) | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
人数 | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 |

成绩分组 | 频数 | 频率(百分比) |
35≤x<38 | 3 | 0.03 |
38≤x<41 | a | 0.12 |
41≤x<44 | 20 | 0.20 |
44≤x<47 | 35 | 0.35 |
47≤x≤50 | 30 | b |
请根据所提供的信息解答下列问题:
(1)频率统计表中a=________,b=_______;
(2)请补全频数分布直方图;
(3)请根据抽样统计结果,估计该次大赛中成绩不低于41分的学生有多少人?




