题目内容
【题目】已知,正方形![]() 的边长为
的边长为![]() 是边
是边![]() 上一动点,连接
上一动点,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 是线段
是线段![]() 的垂直平分线与
的垂直平分线与![]() 的交点,连接
的交点,连接![]() ,并延长
,并延长![]() 交边
交边![]() 于点
于点![]() .
.
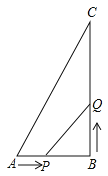
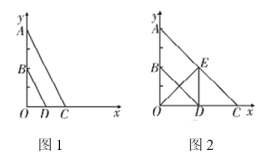
(1)如图1,若![]() 求
求![]() 的度数(用含
的度数(用含![]() 的式子表示);
的式子表示);


(2)如图2,连接![]() 当
当![]() 点运动时,探究
点运动时,探究![]() 的周长是否为定值?若是,求其值;若不是,说明理由;
的周长是否为定值?若是,求其值;若不是,说明理由;
(3)若点![]() 为
为![]() 的中点,则
的中点,则![]() 的面积为 .
的面积为 .
【答案】(1)![]() ;(2)是,其值为12;(3)
;(2)是,其值为12;(3)![]() .
.
【解析】
(1)证明△AGB≌△AGD,得出∠ADG=∠ABF=a,再利用三角形外角的性质即可求![]() 的度数;
的度数;
(2)将△BAF绕B点旋转90°得△BCK,证明△EBF≌△EBK得出EF=EK,即△DEF的周长=DE+DF+FE=DE+DF+EK=AD+DC即可求得;
(3)分别证明△AFG∽△CBG,△AGF∽△BGH利用相似三角形边之间关系,面积与相似比之间的关系即可求解.
解:(1)∵四边形ABCD为正方形,
∴AB=AD,∠BAC=∠DAC=45°,
又∵AG=AG,
∴△AGB≌△AGD,
∴∠ADG=∠ABF=a,
∴![]() ;
;
(2)∵四边形ABCD为正方形,
∴AB=BC,∠BAD=∠BCD=∠ADC=90°,
如下图,将△BAF绕B点旋转90°得△BCK,
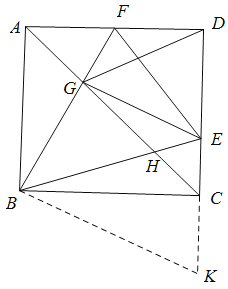
∴CK=AF,∠CBK=∠ABF=a,
∵△AGB≌△AGD,
∴BG=GD,
∵G为BE垂直平分线,
∴BG=GE,
∴BG=GD=GE,
∴∠GED=∠GDE=∠ADC-∠ADG=90°-a,
∴∠DGE=180°-2(90°-a)=2a,
∴∠BGE=∠BGD-∠DGE=2(45°-a)-2a=90°,
∴∠GBE=∠GEB=45°,
∴∠EBK=∠EBC+∠CBK=∠EBC+∠ABF=90°-∠GBE=45°,
在△EBF和△EBK中
∵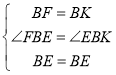
∴△EBF≌△EBK(SAS),
∴EF=EK,
∴△DEF的周长=DE+DF+FE=DE+DF+EK=AD+DC=12.
故△DEF的周长是定值,其长为12.
(3)∵F为AD的中点,
∴![]() ,
,
∵四边形ABCD为正方形,
∴AF∥BC,AD=BC=6,∠BAF=∠ABC=90°,
∴△AFG∽△CBG,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
设△AFG边AF上的高为m,△CBG边BC上的高为n,则m+n=6,![]() ,
,
解得m=2,n=4,
又∵![]() ,
,
∵∠DAC=∠GBE=45°,∠AGF=∠BGC,
∴△AGF∽△BGH,
∴![]() ,
,
∴![]() ,
,
故答案为:![]() .
.

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
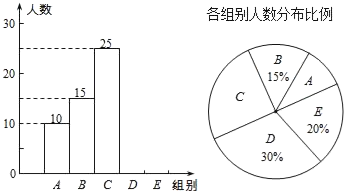
课程达标测试卷闯关100分系列答案【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是 ;
(3)已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.