题目内容
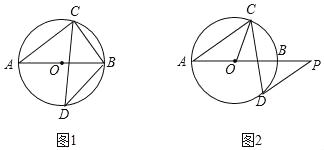
【题目】如图,![]() 、
、![]() 是
是![]() 的中点,
的中点,![]() 平分
平分![]() ,下列结论:①
,下列结论:①![]() 平分
平分![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的结论有( )
,其中正确的结论有( )
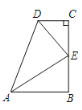
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
【答案】A
【解析】
过点E作EF⊥AD于F,根据角平分线的性质及判定即可证出①;根据平行线的判定证出DC∥AB,然后根据平行线的性质和角平分线的定义即可判断②;根据直角三角形的性质证出ED平分∠CEF,再根据角平分线的性质可得CD=FD,同理可得AB=AF,从而判断③;根据两个三角形等高但不等底即可判断④.
解:过点E作EF⊥AD于F

∵![]() 平分
平分![]() ,
,![]()
∴EF=EB,∠DAE=∠BAE=![]() ∠DAB
∠DAB
∵![]() 是
是![]() 的中点,
的中点,
∴EB=EC
∴EF=EC
∴DE平分∠ADC,故①正确;
∴∠CDE=∠ADE=![]() ∠CDA,
∠CDA,
∵![]()
∴∠B+∠C=180°
∴DC∥AB
∴∠CDA+∠DAB=180°
∴∠DAE+∠ADE=![]() ∠DAB+
∠DAB+![]() ∠CDA=
∠CDA=![]() (∠DAB+∠CDA)=90°
(∠DAB+∠CDA)=90°
∴∠DEA=180°-(∠DAE+∠ADE)=90°
∴![]() ,故②正确;
,故②正确;
∵∠FED=90°-∠ADE=90°-∠CDE=∠CED
∴ED平分∠CEF
∴CD=FD
同理可得:AB=AF
∴AD=AF+FD=AB+CD,故③正确;
∵EF=EB,即△ADE和△ABE等高
但AD≠AB
∴![]() ,故④错误.
,故④错误.
正确的有3个
故选A.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
【题目】甲、乙两台机床同时生产一种零件,在5天中,两台机床每天出次品的数量如下表:
甲 | 0 | 1 | 2 | 0 | 2 |
乙 | 2 | 1 | 0 | 1 | 1 |
关于以上数据的平均数、中位数、众数和方差,说法不正确的是
A. 甲、乙的平均数相等B. 甲、乙的众数相等
C. 甲、乙的中位数相等D. 甲的方差大于乙的方差