ƒøƒ⁄»ð
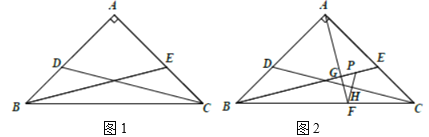
°æƒø°ø“—÷™£¨‘⁄¡‚–ŒABCD÷–£¨G «…‰œþBC…œµƒ“ª∂ص„£®≤ª”ε„B£¨C÷ÿ∫œ£©£¨¡¨Ω”AG£¨µ„E°¢F «AG…œ¡Ωµ„£¨¡¨Ω”DE£¨BF£¨«“÷™°œABF=°œAGB£¨°œAED=°œABC£Æ
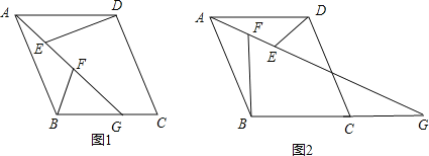
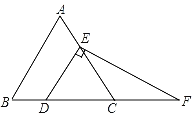
£®1£©»Ùµ„G‘⁄±þBC…œ£¨»ÁÕº1£¨‘Ú£∫
¢Ÿ°˜ADE”ΰ˜BAF______£ª£®ÃÓ°∞»´µ»°±ªÚ°∞≤ª»´µ»°±ªÚ°∞≤ª“ª∂®»´µ»°±£©
¢⁄œþ∂ŒDE°¢BF°¢EF÷ƺ‰µƒ ˝¡øπÿœµ «______£ª
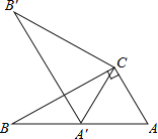
£®2£©»Ùµ„G‘⁄±þBCµƒ—”≥§œþ…œ£¨»ÁÕº2£¨ƒ«√¥…œ√Ê£®1£©¢⁄ÃΩæøµƒΩ·¬€ªπ≥…¡¢¬£ø»Áπ˚≥…¡¢£¨«Î∏¯≥ˆ÷§√˜£ª»Áπ˚≤ª≥…¡¢£¨«ÎÀµ√˜’‚»˝Ãıœþ∂Œ÷ƺ‰”÷‘ı—˘µƒ ˝¡øπÿœµ£¨≤¢∏¯≥ˆƒ„µƒ÷§√˜£Æ
°æ¥∞∏°ø£®1£©¢Ÿ»´µ»£ª¢⁄DE=BF+EF£ª£®2£©DE=BF-EF£¨º˚Ω‚Œˆ
°æΩ‚Œˆ°ø
(1)¢Ÿ∏˘æð¡‚–Œµƒ–‘÷ µ√µΩAB=AD£¨AD°ŒBC£¨”…∆Ω––œþµƒ–‘÷ µ√µΩ°œBGA=°œDAE£¨µ»¡ø¥˙ªªµ√µΩ°œBAF=°œADE£¨«Ûµ√°œABF=°œDAE£¨∏˘æð»´µ»»˝Ω«–Œµƒ≈–∂®∂®¿Ìº¥ø…µ√µΩΩ·¬€£ª
¢⁄∏˘æð»´µ»»˝Ω«–Œµƒ–‘÷ µ√µΩAE=BF£¨DE=AF£¨∏˘æðœþ∂Œµƒ∫Õ≤Óº¥ø…µ√µΩΩ·¬€£Æ
(2)”Î(1)Õ¨¿Ì÷§°˜ABF°’°˜DAEµ√AE=BF£¨DE=AF£¨”…AF=AE-EF=BF-EFø…µ√¥∞∏£Æ
(1)¢Ÿ°þÀƒ±þ–ŒABCD «¡‚–Œ£¨
°ýAB=AD£¨AD°ŒBC£¨
°ý°œBGA=°œDAE£¨
°þ°œABC=°œAED£¨
°ý°œBAF=180![]() -°œABC -°œBGA =180
-°œABC -°œBGA =180![]() -°œAED -°œDAE =°œADE£¨
-°œAED -°œDAE =°œADE£¨
°þ°œABF=°œBGF£¨°œBGA=°œDAE£¨
°ý°œABF=°œDAE£¨
°þAB=DA£¨
°ý°˜ABF°’°˜DAE(ASA)£ª
¢⁄°þ°˜ABF°’°˜DAE£¨
°ýAE=BF£¨DE=AF£¨
°þAF=AE+EF=BF+EF£¨
°ýDE=BF+EF£Æ
π ¥∞∏Œ™£∫»´µ»£¨DE=BF+EF£ª
(2)DE=BF-EF£¨
»ÁÕº£¨
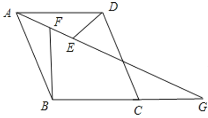
°þÀƒ±þ–ŒABCD «¡‚–Œ£¨
°ýAB=AD£¨AD°ŒBC£¨
°ý°œBGA=°œDAE£¨
°þ°œABC=°œAED£¨
°ý°œBAF=180![]() -°œABC -°œBGA =180
-°œABC -°œBGA =180![]() -°œAED -°œDAE =°œADE£¨
-°œAED -°œDAE =°œADE£¨
°þ°œABF=°œBGF£¨°œBGA=°œDAE£¨
°ý°œABF=°œDAE£¨
°þAB=DA£¨
°ý°˜ABF°’°˜DAE(ASA)£ª
°ýAE=BF£¨DE=AF£¨
°þAF=AE-EF=BF-EF£¨
‘ÚDE=BF-EF

 ¡¡µ„º§ªÓæ´±ý÷”≈100∑÷¥Û ‘æÌœµ¡–¥∞∏
¡¡µ„º§ªÓæ´±ý÷”≈100∑÷¥Û ‘æÌœµ¡–¥∞∏