Question

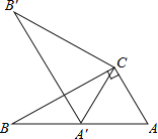
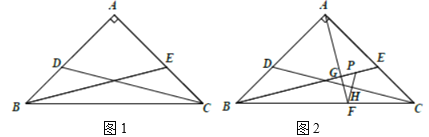
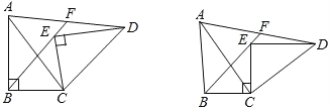
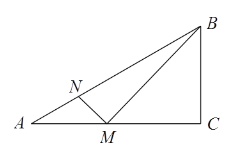
【题目】如图，在△ABC中，∠ABC=90°，将△ABC绕点C顺时针旋转得到△DEC，连接AD，BE，延长BE交AD于点F．

（1）求证：∠DEF=∠ABF；

（2）求证：F为AD的中点；

（3）若AB=8，AC=10，且EC⊥BC，求EF的长．

Answer 1

【答案】（1）见解析；（2）见解析；（3）

【解析】

（1）根据等角的余角相等证明即可；

（2）如图1中，作AN⊥BF于N，DM⊥BF交BF的延长线于M，首先证明△ANB≌△DME，可得AN=DM，然后证明△AFN≌△DFM，求出AF=FD即可；（3）如图2中，作AN⊥BF于N，DM⊥BF交BF的延长线于M，想办法求出FM，EM即可．

（1）证明： ∵CB=CE，

∴∠CBE=∠CEB，

∵∠ABC=∠CED=90°，

∴∠DEF+∠CEB=90°，∠ABF+∠CBE=90°，

∴∠DEF=∠ABF．

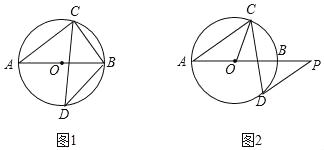
（2）证明：如图1中，作AN⊥BF于N，DM⊥BF交BF的延长线于M．

∵∠ABN=∠DEM，∠ANB=∠M=90°，AB=DE，

∴△ANB≌△DME（AAS），

∴AN=DM，

∵∠ANF=∠M=90°，∠AFN=∠DFM，AN=DM，

∴△AFN≌△DFM（AAS），

∴AF=FD，即F为AD的中点；

（3）如图2中，作AN⊥BF于N，DM⊥BF交BF的延长线于M．

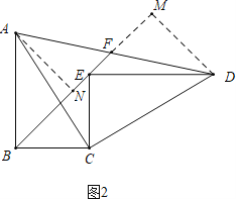
在Rt△ABC中，∵∠ABC=90°，AC=10，AB=8，

∴BC=EC==6，

∵EC⊥BC，

∴∠BCE=∠ACD=90°，

∵AC=CD=10，

∴AD=10，

∴DF=AF=5，

∵∠MED=∠CEB=45°，

∴EM=MD=4，

在Rt△DFM中，FM==3，

∴EF=EM-FM=．